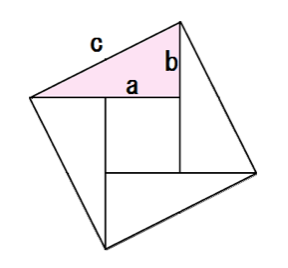
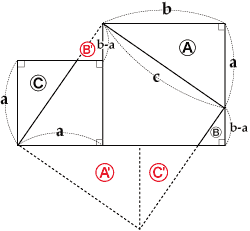
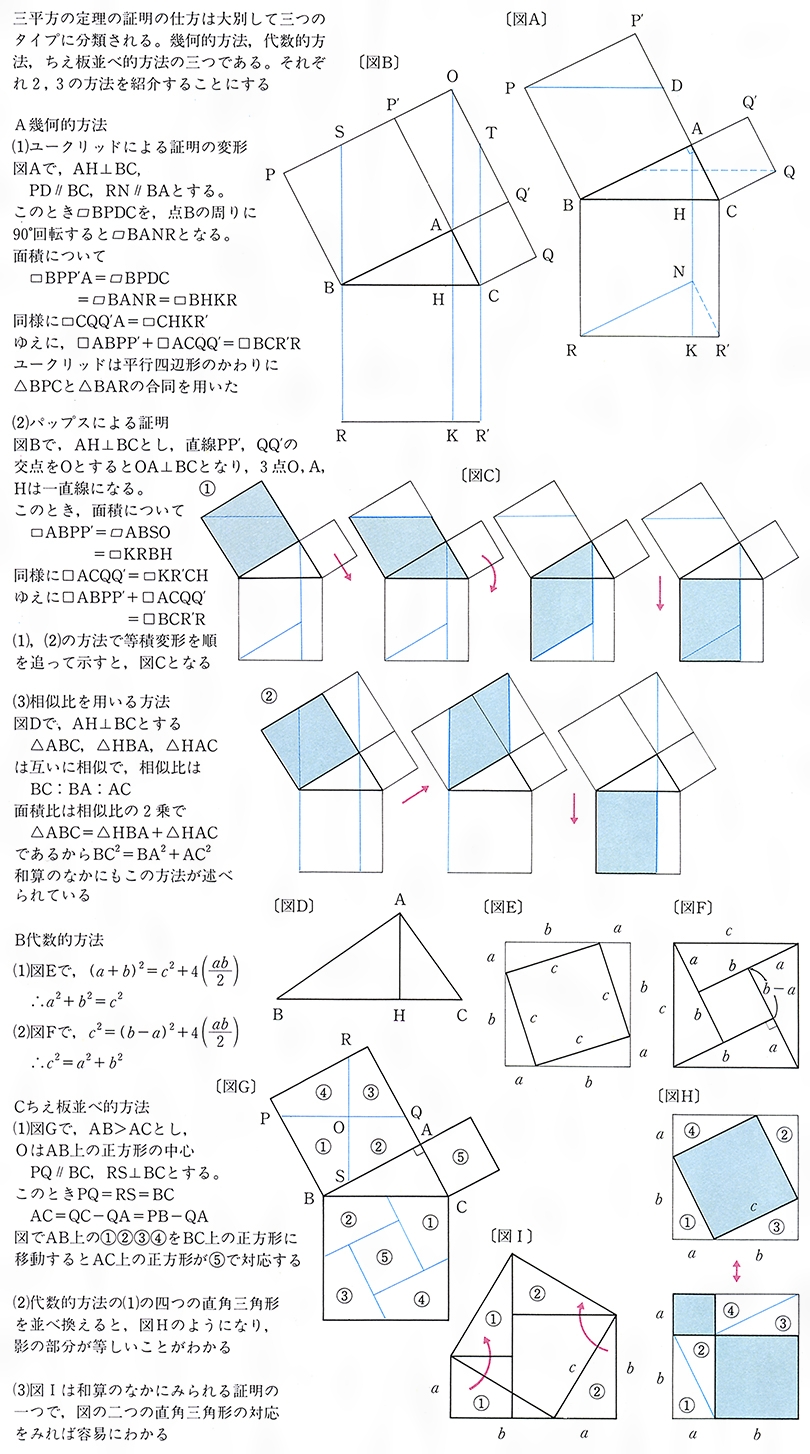
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう三平方の定理の証明<6> 太線の正方形の面積を (ア)外側の1辺×1辺と考えると (a+b)2 (イ)cを1 辺とする正方形の面積と 4 つの直角三角形の面積の 合計と考えると c2+a×b××4 (ウ)(ア)と(イ)は同じ面積を表しているので (a+b)2=c2+2abしたがって,a2+b2=c2直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係はピタゴラスの定理(三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当にピタゴラス(cBC570cBC500)が発見したかどうか確証があるわけではありません。
Tikz 三平方の定理 ピタゴラスの定理 とその証明 数樂管理人のブログ
三平方の定理 証明 円
三平方の定理 証明 円- どこまで、『三平方の定理の証明』を調べるか? 僕個人では、3通りの証明を、自分の中に体取、体得でき、その細部をこうして表現出来れば良いかと考えた。 此処まで、2通りの証明を紹介した。 1、等積変形に依る三平方の定理の証明三平方の定理の逆を証明する 三平方の定理の逆って、なんで成り立つの? 証明はどうすんの? ってことをお話していきます。 3辺の長さが の三角形において が成り立つならば、 ABCはcを斜辺とする直角三角形となることを証明せよ。 まずは、 が




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
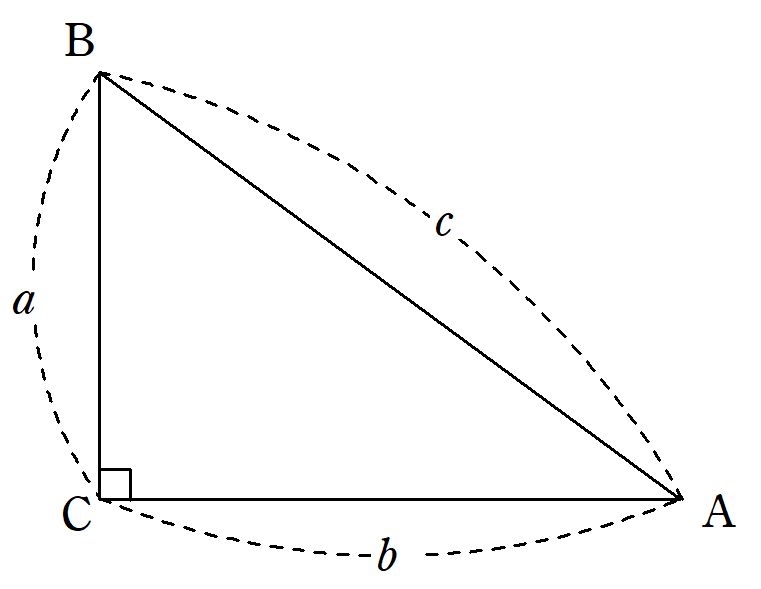
三平方の定理(ピタゴラスの定理) ∠ACB=90°となる直角三角形ABCにおいて,各辺の長さを, BC = a , CA = b , AB = c とすると, a 2 b 2 = c 2 の関係が成り立つ.この関係を 三平方の定理 あるいは ピタゴラスの定理 という. 証明三平方の定理を用い て,問題を簡潔に解決し たり,発展させたりでき る。 三平方の定理の証明 を読みとったり,表した りすることができる。 三平方の定理を用い て,線分の長さ,面積, 体積を求めることがで きる。三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べて正方形ABDFをつくる。 正方形ABDFの面積をSとすると、1辺がcなので S=c2 ① また、正方形ABDFは ABCと合同な三角形4つと正方形EGHCでできている。 ABCの面積は 1
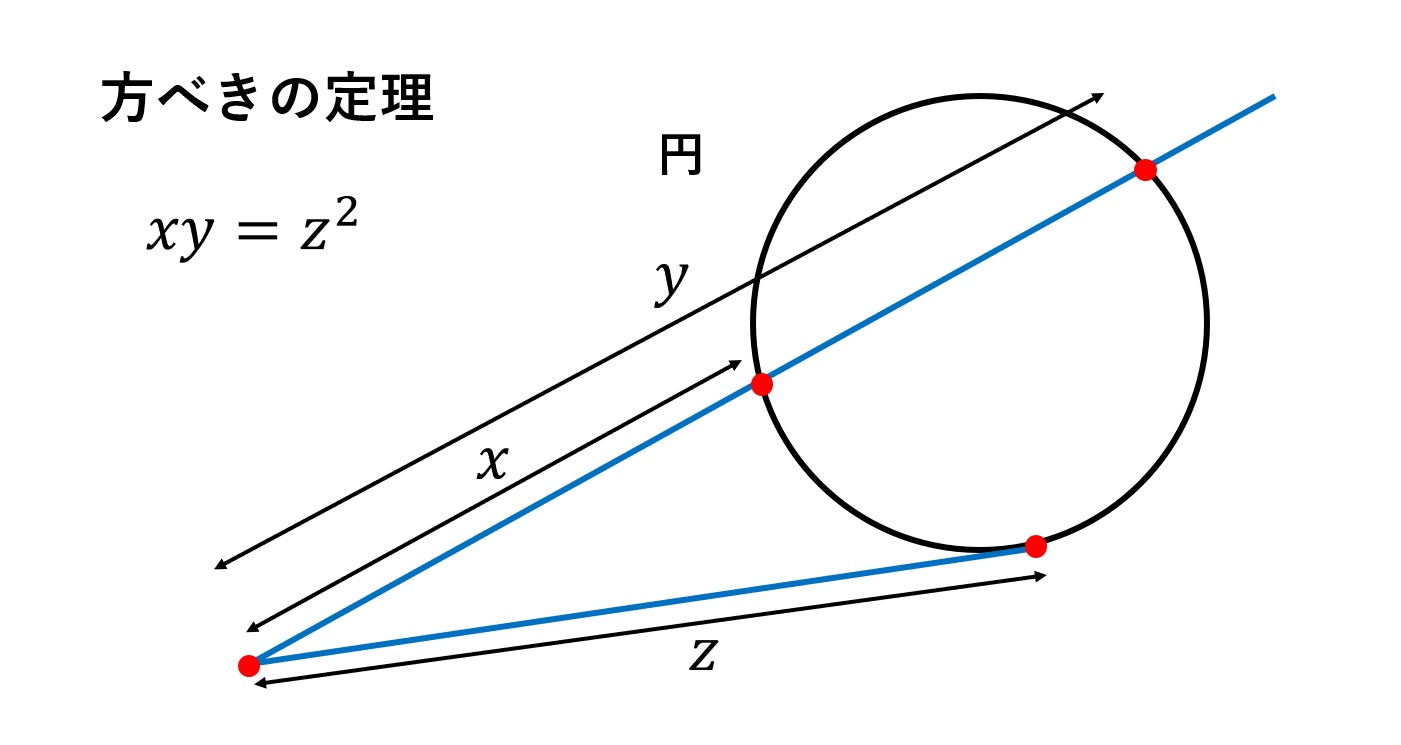
三平方の定理の最も変わった証明方法はなんですか? 既に回答があるように, 三平方の定理は数多く知られています。しかし, 三平方の定理があまりにも基本的な性質なので, 変わった証明を考えるのは困難です。変わったことをしようとすると, 実は三平方が成り立ちます.(これを三平方の定理といいます.) 逆に,三辺の長さについて, a 2 b 2 =c 2 が成り立つとき,その三角形は直角三角形です. (これを三平方の定理の逆といいます.) 一番長い辺三平方の定理 \\ x^2y^2 \\ を満たす整数は無数にある. \\( 3^24^2=5^2 \\), \\(5^212^2=13^2\\) この両辺を z^2 で割った \\ (\\frac{x}{z
三平方の定理には数百もの証明方法があります。今回は相似を利用した2つ目の証明方法について紹介します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴラスの定理 三平方の定理には数百もの証明方法があります。今回は中3の教科書でよく見かける2つの証明方法について解説します。 Ⅰ 三平方の定理とは 三平方の定理とは、次のような定理です。 三平方の定理(ピタゴ中学数学(三平方の定理):証明(図形的に) 数学(中学) 対象 高校生 再生時間 816 説明文・要約 ・「正方形の面積を移す」という観点で三平方の定理が成り立つことを示すもの (この他にも証明方法はいくつかあります) 関連動画




三平方の定理の4通りの美しい証明 高校数学の美しい物語



三平方の定理
証明の方針:「相似な図形の面積は対応する部分の長さの二乗に比例する」という重要な事実と三平方の定理から s 1 s 2 = s 3 s_1s_2=s_3 s 1 s 2 = s 3 が分かります。三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 1.三平方の定理の証明その1 まずは良く知られた、最もポピュラー(? )な証明方法をご紹介します。 まず、直角三角形ABCを準備します。 長さが𝑎と𝑏(𝑎>𝑏とします)、斜辺を𝑐としましょう。 以降、この直角三角形をベースにお話していき




中学数学 三平方の定理




三平方の定理の証明 相似を利用した証明2 Fukusukeの数学めも
ですから, 余弦定理の場合は − 2 b c cos θ の項が三平方の定理に付け加えられているだけですね. つまり, ∠ A が 90 ∘ から θ に変わると,三平方の定理の等式が − 2 b c cos θ 分だけズレるということになっているわけです. このように見る 三平方の定理の1つの証明 作成者 nunokazu ステップ1→2→3、およびステップ4→5→6にボタンを押すか、スライダーを動かして、2つの正方形と同じ面積を大きな正方形の上に移す様子を観察しましょう。 これらの動きを書き表すと、三平方の定理の1つの証明三平方の定理の逆とは、三角形の3辺がa² b² = c² を満たせば、その三角形は直角三角形であるというものです。図形の証明問題などに使われる場合があるので、覚えておきましょう。 三平方の定理の証明




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理 おやじさん ネット
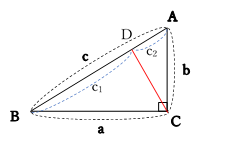
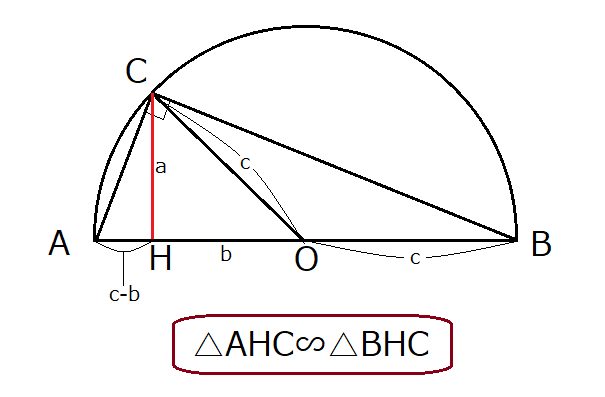
三平方の定理 三平方の定理(1) 1 次の図でxの値を求めなさい。 374 3㎝ 4㎝ 三平方の定理より x =4 +3 =16+9 = x >0だから x = 答え x 2 2 2 2 次の図でxの値を求めなさい。 3 次の長方形の対角線の長さを求めなさい。 対角線の長さをx ㎝とすると 三平方の定理より、三平方の定理の証明 いろいろな種類40通りの証明を行いました。 丁寧とはいえない書き方のものもありますが、各自補って読んでください。 三角形三平方の定理の証明<2C> 三平方の定理の証明<3> (アインシュタインが小学生の時に見つけたといわれる証明) AB BC CA= , = , = とするとc a b ∽ ∽ となりABC CBD ACD 斜辺の長さを利用して 相似比は : :c a b 面積比=(相似比) なので2




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理の4通りの美しい証明 高校数学の美しい物語
ピタゴラスの定理の証明を集めた本は多数あるが,今回の記事を書くにあたり,『ピタゴラスの定理 $100$ の証明法 ― 幾何の散歩道』(森下四郎著,プレアデス出版)を参考にした.証明が種類別に分けられ,系統的に説明されていて分かりやすい.考えていて楽しくなるような,趣向を凝らし



Http Www Shimanet Ed Jp Minami Link Homepage Naga005 Pc Mathekyouzai001 Sanheihou Theorem Pdf




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月




3分で理解 三平方の定理 ピタゴラスの定理 とその証明を完全解説 Rikeinvest



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook



ピタゴラスの定理とその証明




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



コラム ピタゴラスの定理 江戸の数学



三平方の定理




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三平方の定理の証明と使い方




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理の証明 直感的に分かる図で解説します 数学fun




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ



1




三平方の定理について考える3 文教出版巻末の 数学研究室 より 身勝手な主張



三平方の定理の最も変わった証明方法はなんですか Quora




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




三平方の定理の証明と使い方



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋




数学を愛する会 本発売 三平方の定理の証明 物理
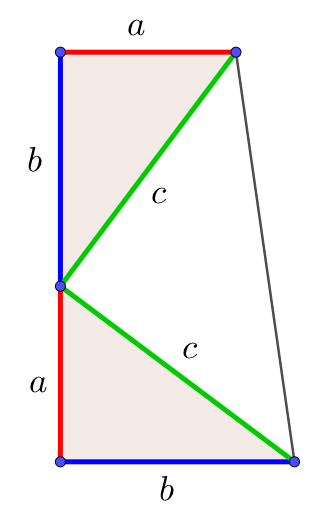



三平方の定理の証明3 大統領の台形 キソカラ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



1



Tikz 三平方の定理 ピタゴラスの定理 とその証明 数樂管理人のブログ




ピタゴラスの定理 Wikipedia




三平方の定理 ピタゴラスの定理 東大合格コム
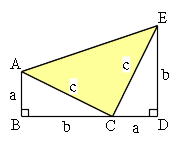



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




てなぐさみのメモ 三平方の定理と素因数分解と円の接線




数学 三平方の定理 中学生 数学のノート Clear



三平方の定理とは コトバンク




ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理の証明と使い方
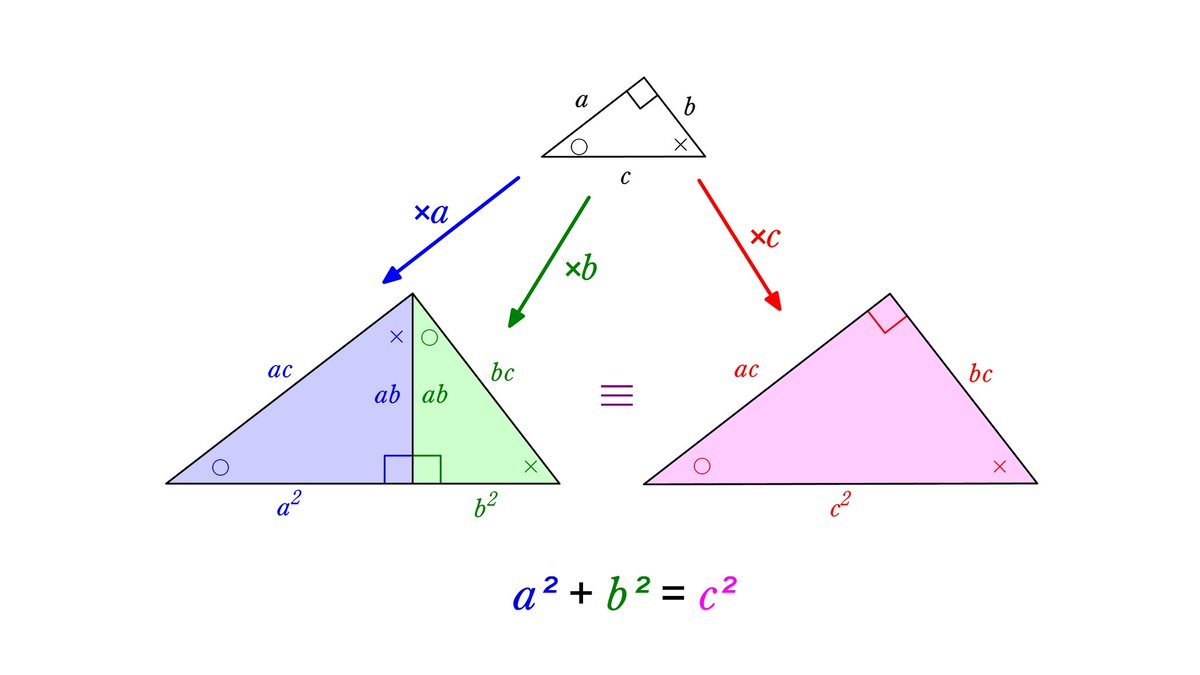



ポテト一郎 三平方の定理 一番好きな証明です




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
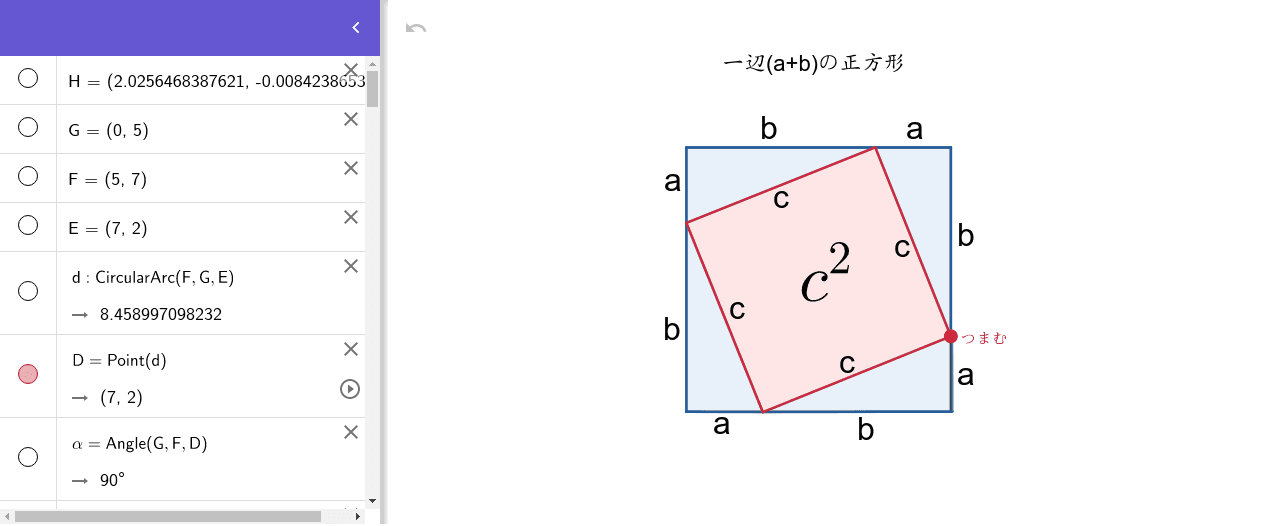



三平方の定理 証明 Geogebra




三平方の定理 ピタゴラスの定理 の証明まとめ5選 全部でいくつあるの 遊ぶ数学
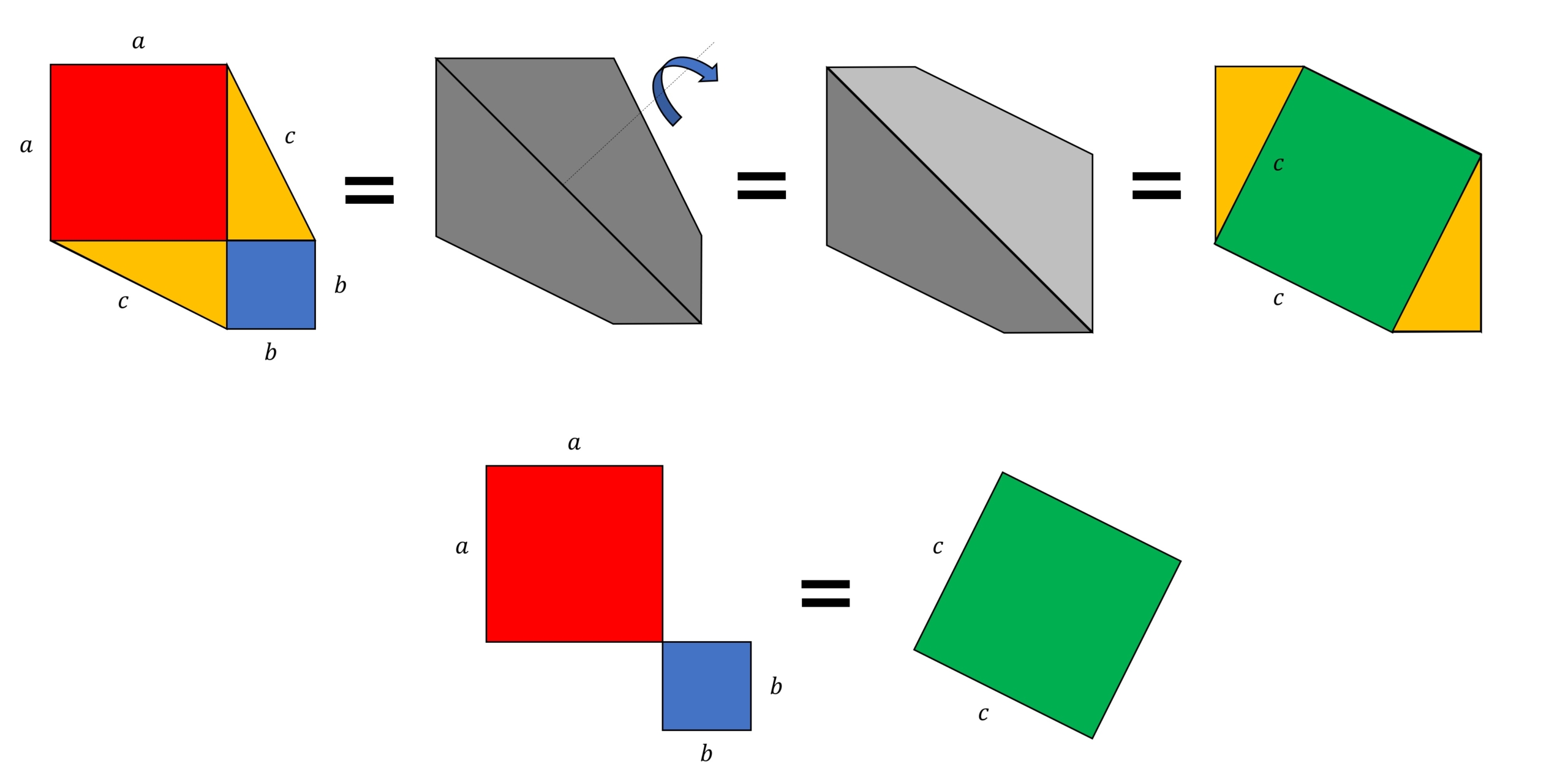



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




ピタゴラスの定理 の証明アニメ2 ピタゴラス自身による証明 Youtube




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理 ピタゴラスの定理 の歴史 素朴に考えてみよう



三平方の定理の証明 ピタゴラスの証明 Fukusukeの数学めも




三平方の定理について考える1 教科書 大日本図書 の証明方法 身勝手な主張



1



Studydoctor三平方の定理の証明 中学3年数学 Studydoctor



三石 数学塾 三平方の定理の証明 その2




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
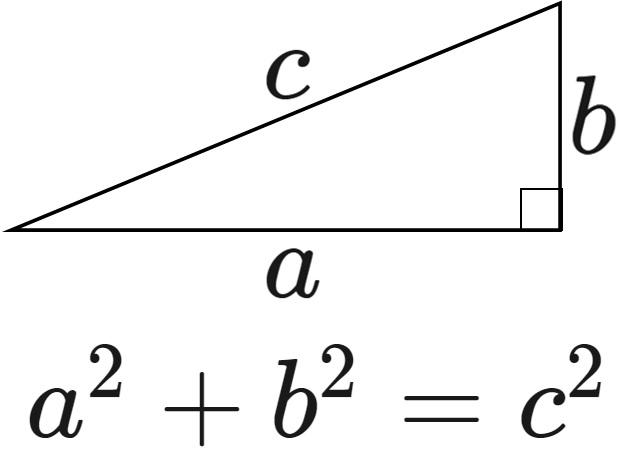



B Oc Hdjqqqofm




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ




三平方の定理 証明の展覧会
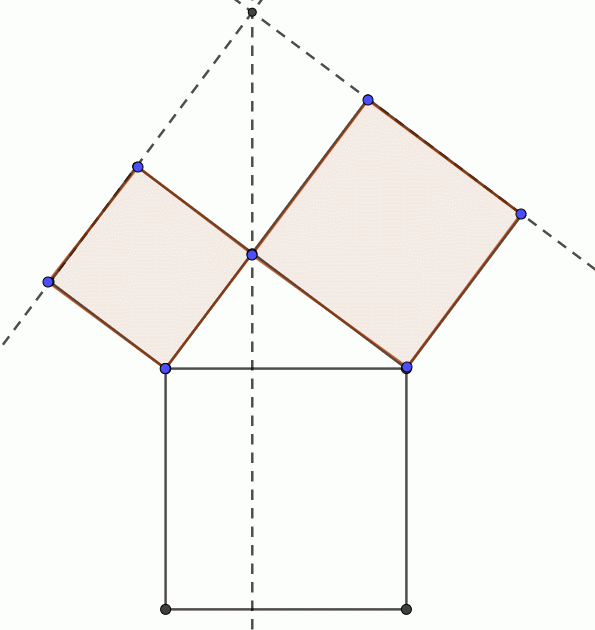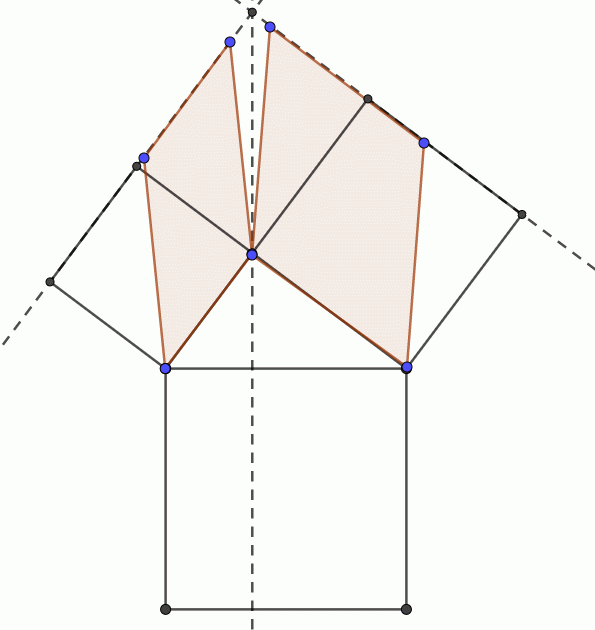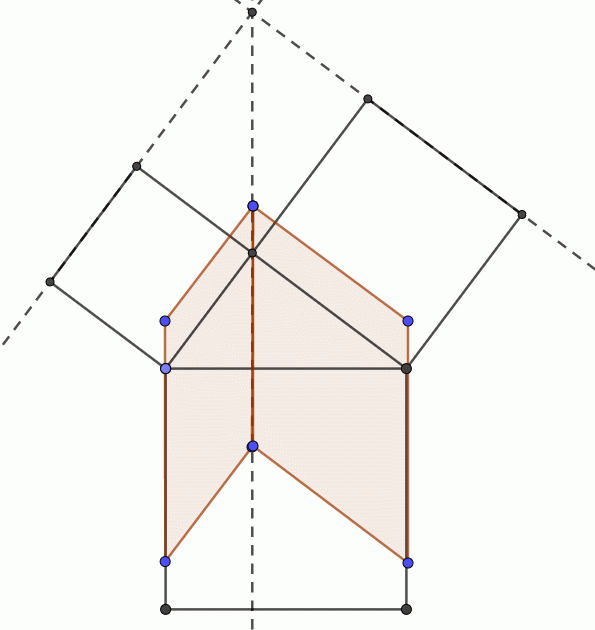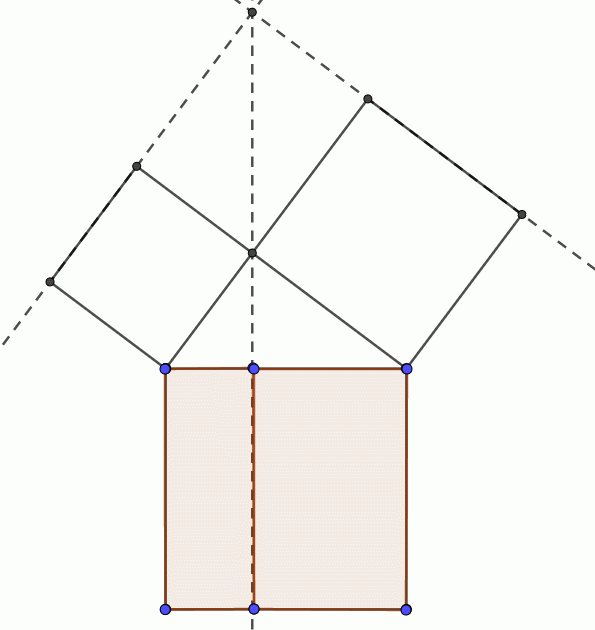



三平方の定理の証明5 だまって平行移動 キソカラ



三平方の定理



三平方の定理



三平方の定理




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2




三平方の定理 の証明 その1 第4話 Factory Takumaro ページ




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ
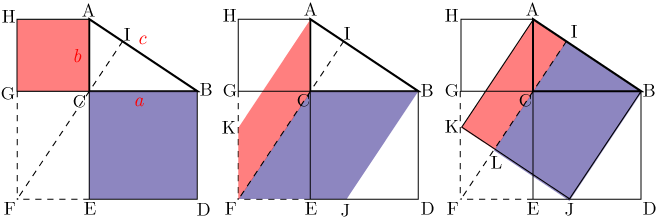



三平方の定理 ピタゴラスの定理




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



中3数学 三平方の定理1 三平方の定理 証明 すべて無料 星組の中学数学講座



証明にこだわる




三平方の定理 膨大なページ数 Wiki




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学
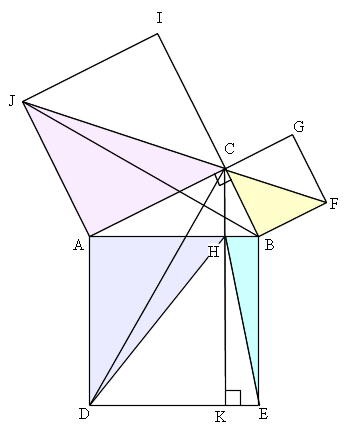



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ



三平方の定理



三平方の定理



1




コラム ピタゴラスの定理 江戸の数学



三平方の定理 アメリカ合衆国大統領の証明 数々のたのしみ




数学 三平方の定理 証明 図形的に オンライン無料塾 ターンナップ Youtube




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




余弦定理 は三平方の定理の進化版 余弦定理は2つある




Catatan Tentang 中学数学 三平方の定理のキホン Junior Clear
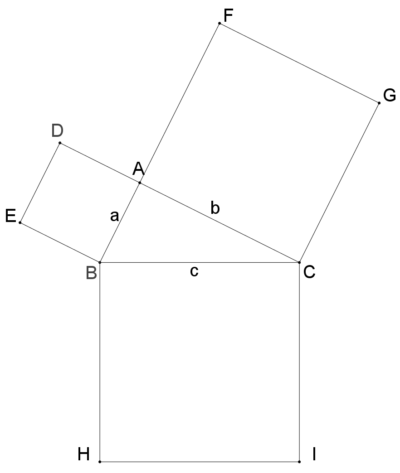



三平方の定理の証明 ユークリッドの証明 Fukusukeの数学めも



三平方の定理の逆の証明




ピタゴラスの定理 Wikipedia




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ



三平方の定理
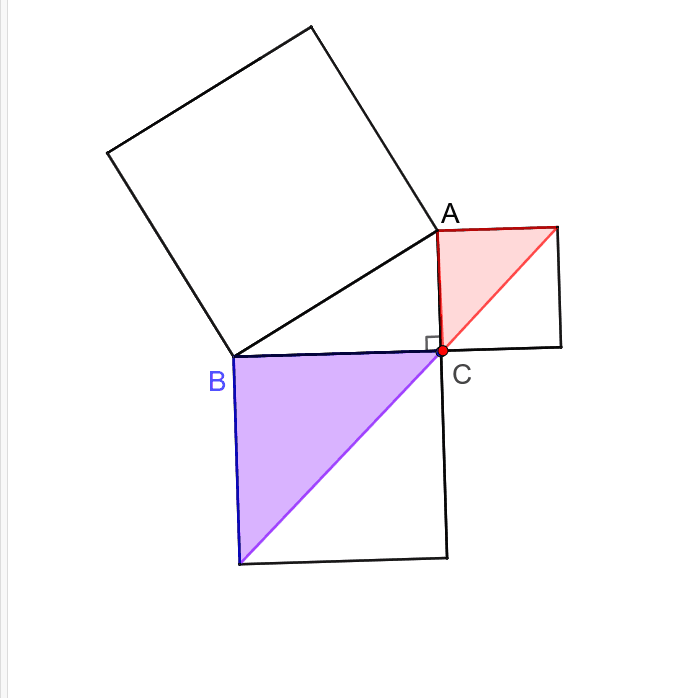



三平方の定理の証明 ユークリッドの証明 Geogebra
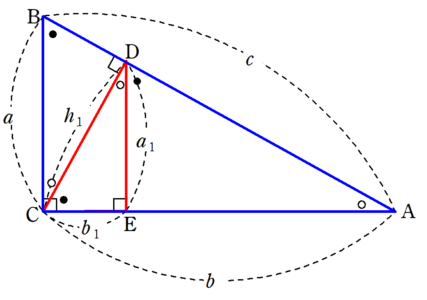



三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも




ひらめき 三平方の定理の証明方法を知ろう 画像で解説 Mathlog



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



参拾萬 Net Functionview 三平方の定理の証明
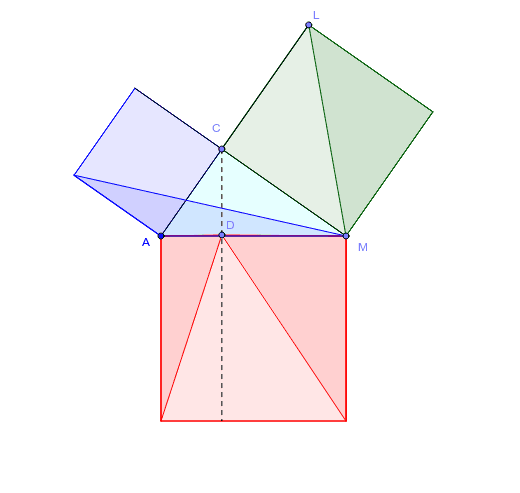



ピタゴラスの定理 ユークリッドの証明 Geogebra



三平方の定理




数学 中3 61 三平方の定理 基本編 Youtube
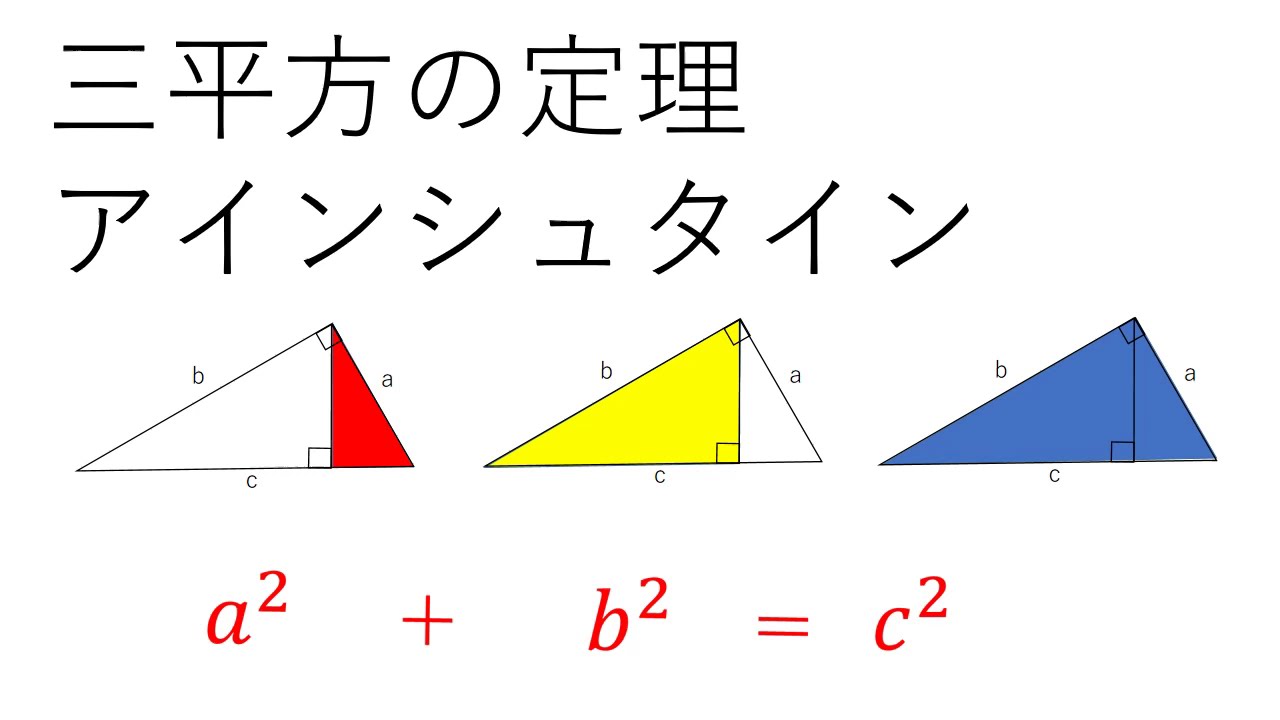



三平方の定理8 アインシュタイン Youtube
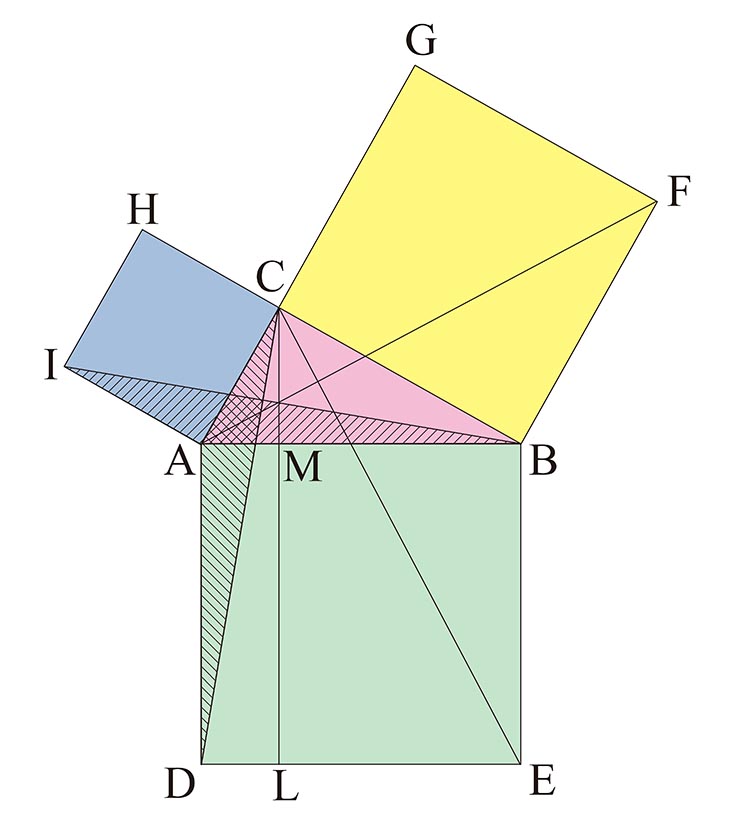



コラム 数学者的思考回路 13 ピタゴラスの定理 証明コレクション




三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト
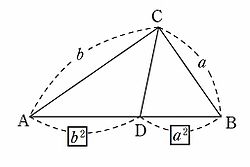



ピタゴラスの定理 Wikipedia



0 件のコメント:
コメントを投稿