2年生 5 図形の性質と証明 知識・技能の習得を図る問題 年 組 号 氏名 全国学力・学習状況調査 A問題 ② 2 下のように「平行四辺形の2組の向かい合う辺はそれぞれ等しい」ことを証明しました。 中学2年の三角形合同の証明で, 合同であることが証明した後の合同な図形の対応する 角は等しいから・・・・ を 単に したがって とか よって で記述しても 正解でしょうか。 お願いします。仮定と結論,逆,合同条件/三角形の合同の証明/二等辺三角形の定理/ 二等辺三角形の性質を使った証明 問題 次の①~④のことがらの中から逆が正しいものをすべて選び,番号を書け。
中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生
三角形証明問題
三角形証明問題-反射テスト 証明問題 三角形 五心とその関係 02 1 をうめよ(s 級2 分30 秒; 三角形の1つの内角の二等分線と他の頂点の外角の二等分線は1点で交わる}}} \\2zh その交点を傍心は{1辺と他の2辺の延長からの距離が等しい点(傍接円の中心)}}である} 1つの三角形の傍心(傍接円)は3個ある\ \ \bm{\mathRM{I_{A}}\,を\ \mathRM{\angle A}内の傍心}という(\mathRM{I_B,\ I_C}\ についても同様) \\1zh



最も人気のある 三角形合同証明 ニスヌーピー壁紙
三角形の合同 三角形の証明練習1 無料で使える中学学習プリント 1 三角形の証明練習 名前 右の図の正方形abcdにおいて、点bと点d を結び、∠adbの二等分線と辺abの交点をeとする。 点eから辺bdに垂線をひき、その垂線と辺bdとの交点 をhとする。反射テスト 証明問題 三角形 五心とその関係 01 1 をうめよ(s 級1 分;だんだん色々な問題を紹介するようになりましたが。 今回は,初心に戻って,非常に図がシンプルだけど,何かキツイ問題です。北海道は,図がシンプルで,証明の書く量もそこまで多くないですが,何か難しい! 第27回芸術的な難問高校入試 「どの三角形」
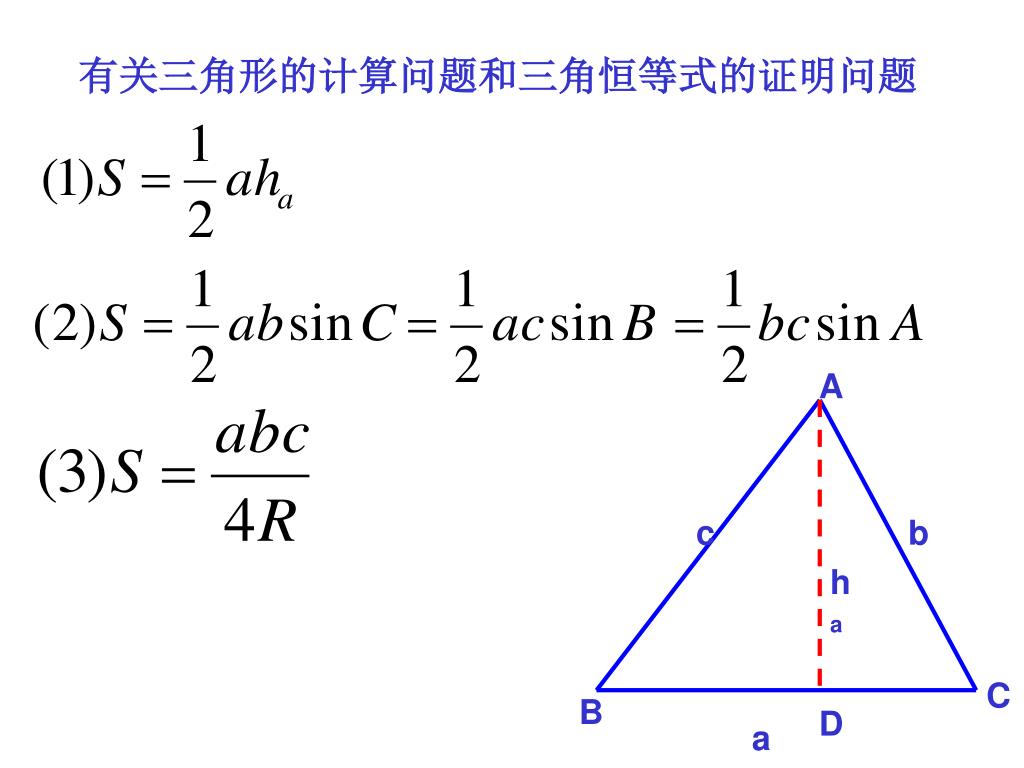
C 級4 分) a b d c f e i 定義 三角形の全ての辺に接する円を内接円といい;三角形の形状・証明問題 == 《解説》 三角形の形状問題(正三角形,二等辺三角形,直角三角形など三角形の種類を言い当てる問題)や証明問題においては,正弦定理や余弦定理を変形して,角度に関する式を辺に関する式に直してから考えるのが原則です中2数学。三角形の「合同」を証明せよ。ヤバい図形のどこを見れば? 仮定?「=」の使い方のルール? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 証明がサクサク進む。数学のコツを公開だ。
三角形の鋭角・直角・鈍角条件、三角形の成立条件3パターン 変数変換による平均値・分散・標準偏差・共分散・相関係数の変化 角の大きさ (辺の長さ)は等しいので ( ∠ B D C =180°<一直線>より) ∠ A D B = ∠ A D C =90° = B D = C D となり 「二等辺三角形の 頂角の二等分線は底辺を垂直に二等分する」 を証明することができました これらの定理は 「証明の問題」以外でも ※三角形の重心 定義と性質を証明問題と座標を用いる例題で解説! 円の性質もしっかり復習しておきましょう! 記事の内容でわからないところ、質問などあればこちらからお気軽にご質




中考数学 三角形证明 题型总结 5



玩转初中几何 等边三角形衍生问题的多种解法探究 中学数学研究会 微信公众号文章阅读 Wemp
C 級8 分) a b c i s u t ★三角形の内心 三角形の内心は;その中心を外心という ★ abc の は def の である 正三角形ではなく、cb=ca,cd=ce,∠acb=∠dceの二等辺三角形の場合もあります。 直角三角形 直角三角形から直線に垂線を引いたパターンです。 三角形の内角の和が180°であること、直線が180°であることを利用します。 平行四辺形(1) 平行四辺形と直角三角形の



数学の証明問題の解き方 セルモ大蔵 世田谷 の塾長ブログ




初一数学几何练习题 含答案
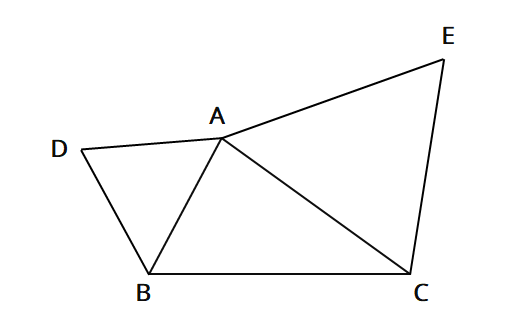
第2学年 5 図形の性質と証明 (2) (1)とは別の三角形に着目して,証明することにしました。 ACDと ABEに着目して, CD=BEであることを証明しなさい。 (3) この問題で,CD=BEは常にいえることが何かと嫌がられる証明問題ですが、書き方(流れ)を覚えると、効率の良い得点源になります。 上にある テンプレート(解答用紙)と動画内で紹介する素材を使えば $\textcolor{blue}{90}$ %以上の証明問題は解けます。 証明問題は計算ミスもなく、簡単な問題でも配点が大きいものとなるので 問題 三角形abcがある。辺ac上に点dをとり、点dを通る線で三角形abcを折り、点aを辺bc上に重ね、重なった点を点eとする。点dを通る線と辺ab上の交点をfとする。 ∠afd=∠febのとき、 cdeは二等辺三角形となることを証明しなさい。 ⇒解答例はこちら(jpg画像)



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




中2数学 三角形の合同の証明の解き方の手順 こいがくぼ翼学習塾
中学2年生 数学 三角形 練習問題プリント 無料ダウンロード・印刷 合同条件などをもとにして三角形の基本的な性質を論理的に確かめたり、図形の性質の証明から新たな性質を見出す方法を、練習できる問題プリントです。証明問題で二等辺三角形があるとき 証明問題で二等辺三角形があるとき、 どの \(2\) 辺が等しい二等辺三角形なのか、情報が与えられます。 そのとき、 「二等辺三角形なので、底角は等しい」 は証明なしで使ってOKです。三角形の形状問題も,角度に関する式を辺に関する式に直してから考えるのが基本です. a=b など a=b の→二等辺三角形 a 2 =b 2 c 2 など→ ∠A=90° の直角三角形 などど答えます.



三角形内角和为180度 这个问题数学家研究了两千多年 凑要教育网
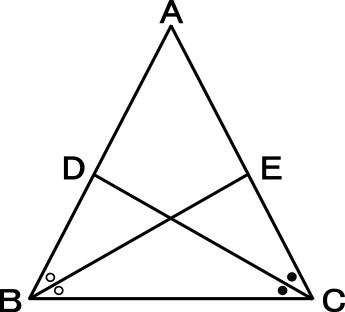



中学2年数学練習問題 図形と合同 三角形の合同の証明問題
三角形の合同の証明 三角形の合同の証明③ 下の図で,ac°db,cm=dm である。 このとき,¼acm×¼bdm であること を右のように証明した。下線部をうめて, 証明を完成させなさい。 三角形の合同の証明④ 下の図で,ab°dc,ab=cd である。3 つの角の二等分線は必ず1 点で交わる 証明 三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは、



证明两个三角形全等的基本思路第2怎么写 信息图文欣赏 信息村 K0w0m Com



建议收藏 全等三角形证明中辅助线做法大全 相似三角形证明方法大全
① 合同な三角形を2つ1組として3組6個 をランダムに配列して与え,合同な三角形を 示し,そこで成立している合同条件を答え る。 ↓ 3 演繹的に推論する ② 三角形の合同を証明する問題において,ま ず仮定と結論を明らかにする。 ↓




正三角形の合同証明 無料で使える中学学習プリント




4ic91kxbqrs6qm
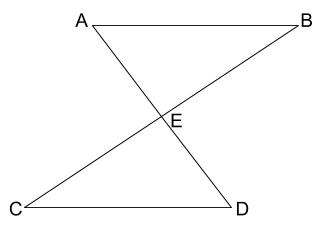



中学数学 三角形の合同の証明 その1 中学数学の無料オンライン学習サイトchu Su
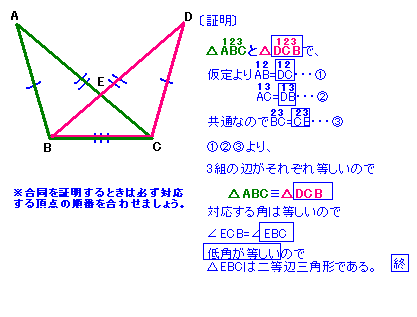



証明問題424 三角形の合同 中学数学の問題を解くコツ




中考数学 三角形证明 题型总结 4
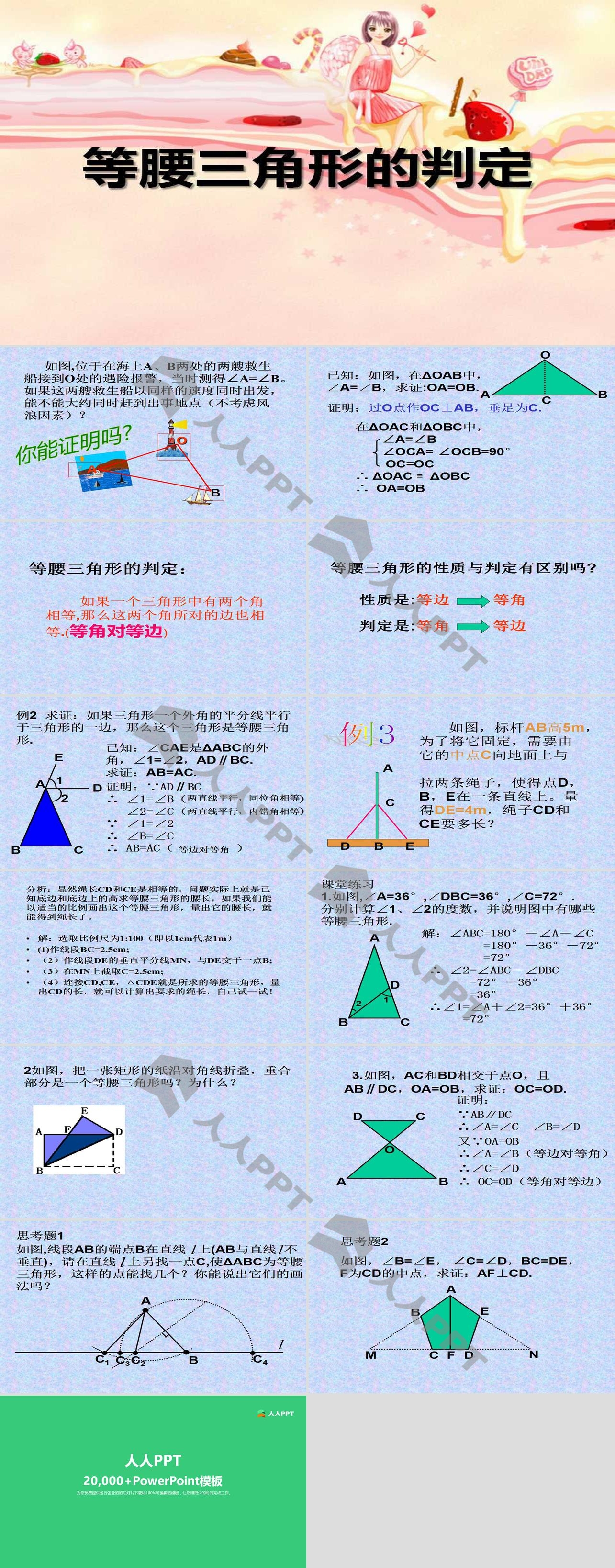



等腰三角形的判定 轴对称ppt课件 Ppt课件下载 人人ppt




中2数学 正三角形の証明 練習編 映像授業のtry It トライイット
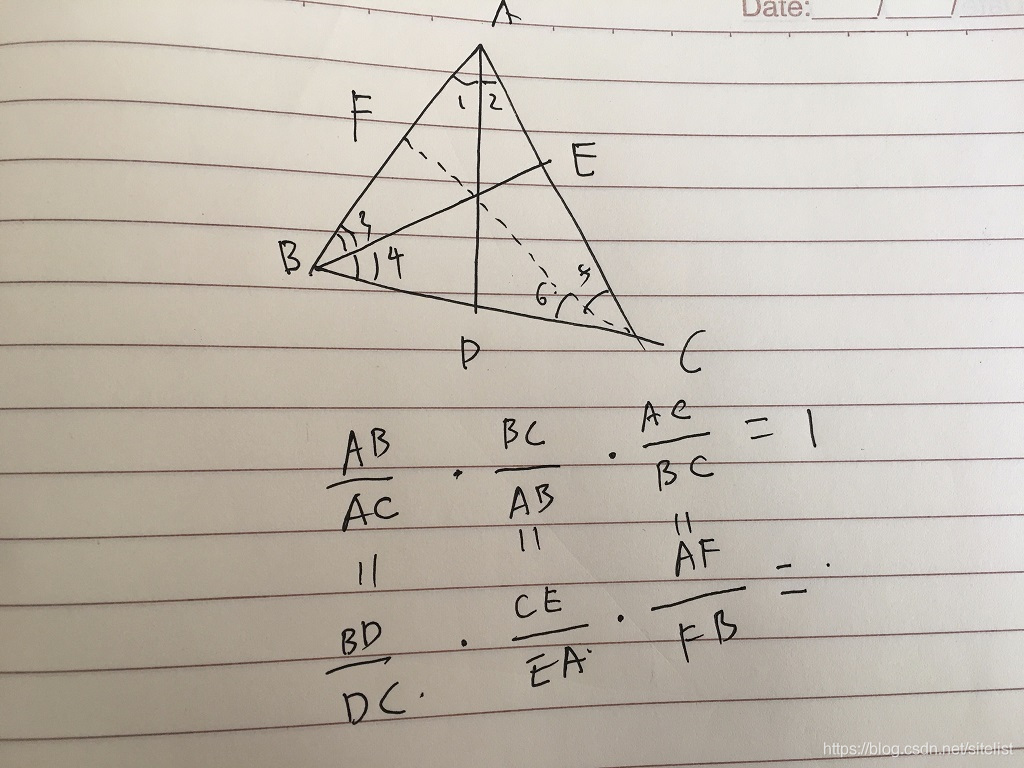



平面几何 赛瓦定理证明三角形的三条垂线或中线或角平分线三线共点问题 Linux 0 11调试教程 程序员宅基地 程序员宅基地
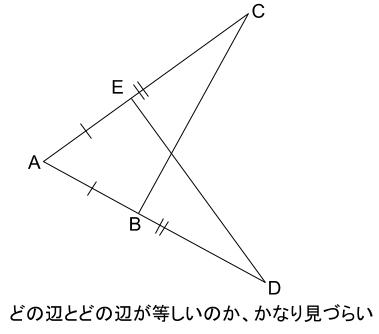



最も人気のある 三角形合同証明 ニスヌーピー壁紙



全等三角形例题50道全等三角形经典证明 都会了遇到三角形的题绝对没问题 尚书坊




中2数学 三角形の合同を証明する問題 練習編 映像授業のtry It トライイット
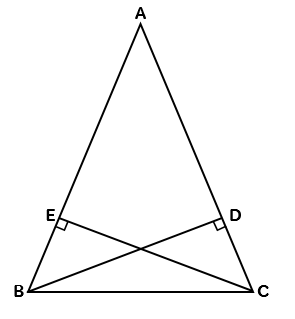



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
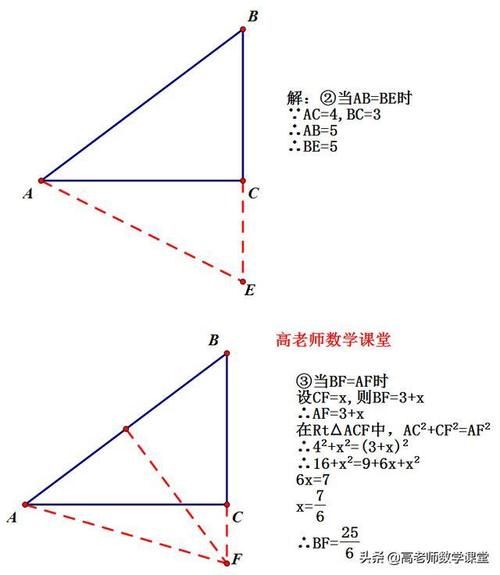



直角三角形证明题个



建议收藏 全等三角形证明中辅助线做法大全 相似三角形证明方法大全




中考数学 三角形证明 题型总结 6




初中全等三角形知識點 每日頭條



初中数学 证明复杂三角形全等的绝好思维方式 谁掌握谁受益




平面几何 赛瓦定理证明三角形的三条垂线或中线或角平分线三线共点问题 Linux 0 11调试教程 程序员宅基地 程序员宅基地




最も人気のある 三角形合同証明 ニスヌーピー壁紙



中2数学 学年末テストの証明問題よく出るパターンをまとめてみた 個別指導塾のyou 学舎日記 公式ブログ



三角形外角 数学作业 解题作业帮



初一数学题 关于三角形内角和 全等三角形的问题 数学作业 解题作业帮
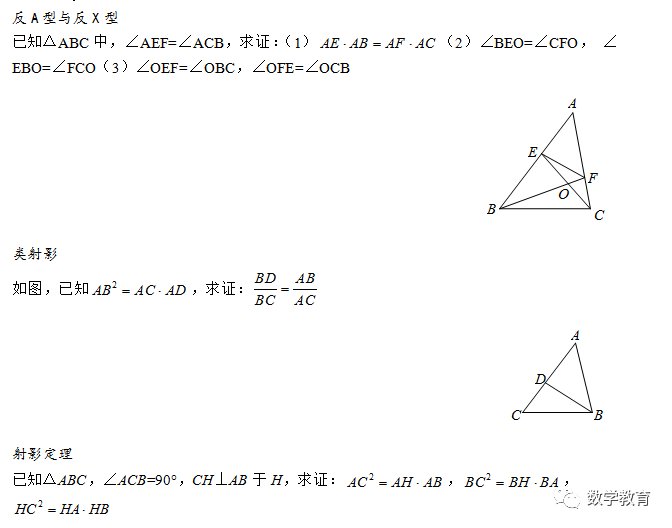



X型相似三角形的证明




中考数学 三角形证明 题型总结 2
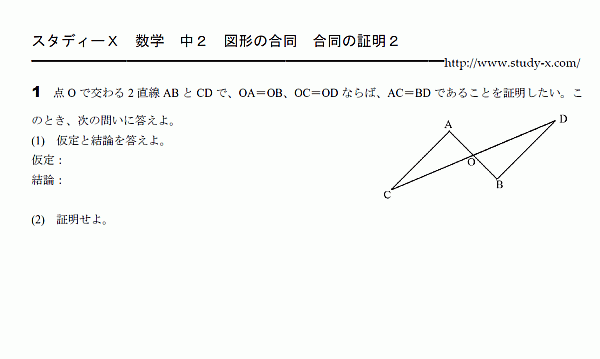



中2 数学 無料学習プリント教材



全等三角形例题50道全等三角形经典证明 都会了遇到三角形的题绝对没问题 尚书坊
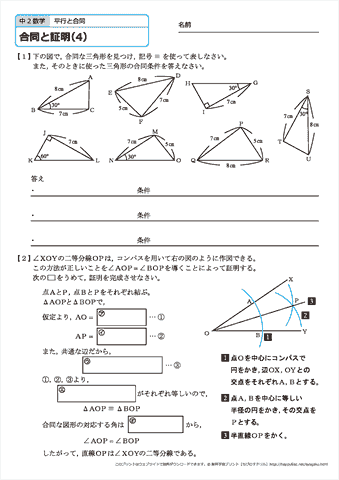



最も人気のある 三角形合同証明 ニスヌーピー壁紙




直角三角形と証明 Youtube
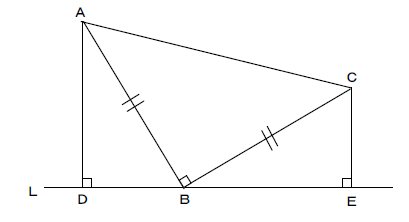



中2数学 直角三角形の合同条件を使った証明の定期テスト過去問分析問題 Atstudier




合同の証明 清水塾




中学2年生 数学 三角形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



全等三角形证明方法归纳 典例详解几种辅助线做法 含思路分析 电竞主播网



Ppt 解三角形应用举例1 Powerpoint Presentation Free Download Id



建议收藏 全等三角形证明中辅助线做法大全 相似三角形证明方法大全
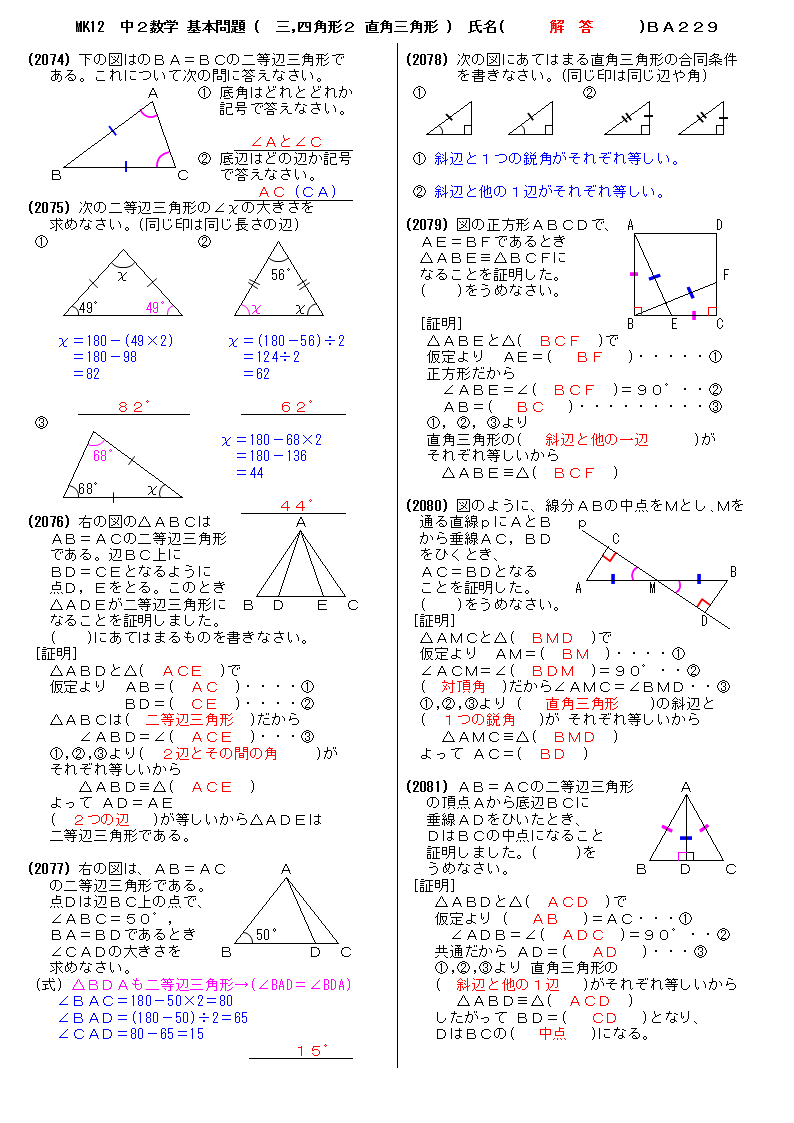



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形




如何逐步进行几何证明 科学 21




中学2年生 数学 合同と証明 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




初中几何相似三角形的判定定理与相关性质 星火网校



文章 例谈等边三角形问题的证明 32 1等腰三角形的性质定理和判定定理及其证明 初中冀教版 数学中国网



建议收藏 全等三角形证明中辅助线做法大全 相似三角形证明方法大全




快乐数学 惊天大秘密 所有三角形都是等腰三角形吗 你能发现问题吗 哔哩哔哩




相似三角形判定定理的证明 图形的相似ppt下载 牛二ppt
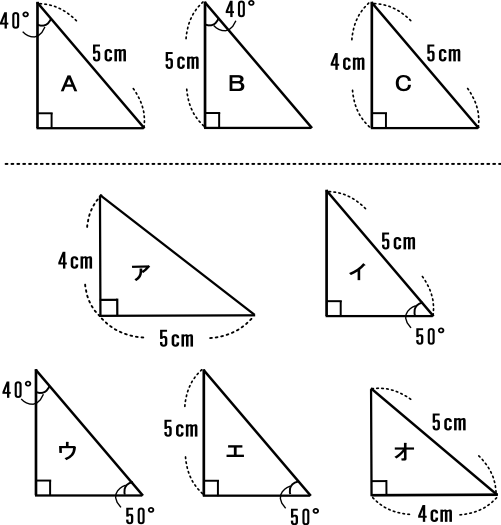



中学2年数学練習問題 直角三角形の合同条件と証明問題 図形と合同



初中三角形中线定理证明三角形中线定理的定理证明 朵拉利品网



几何神书 拯救你的中考几何解题能力 初中数学 小初高题库试卷课件教案网
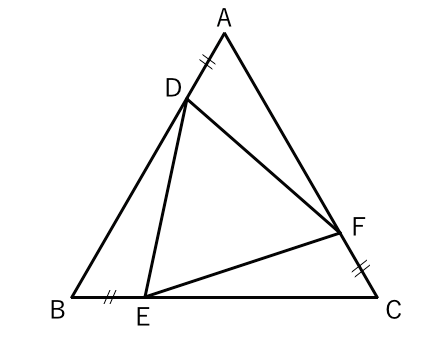



合同な図形 正三角形の証明問題 苦手な数学を簡単に
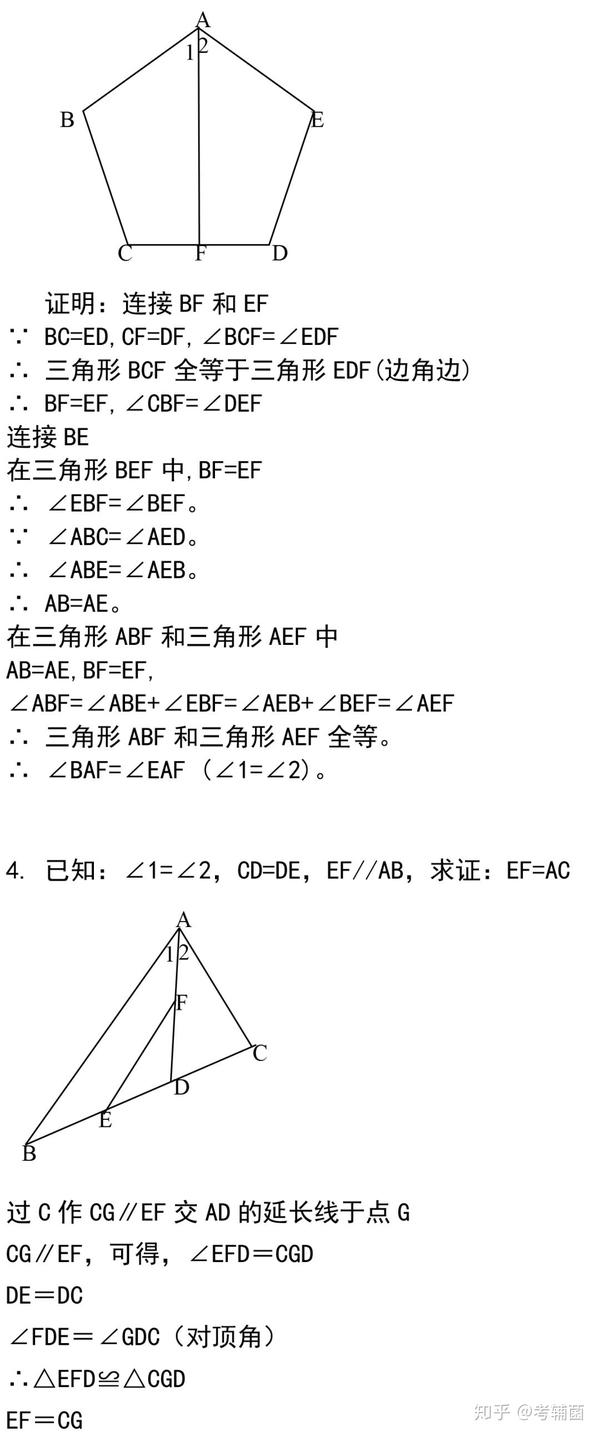



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 知乎




中考数学 三角形证明 题型总结



线段乘积问题必然与相似三角形有关 遇到了数学



证明两个三角形全等的基本思路第2怎么写 信息图文欣赏 信息村 K0w0m Com
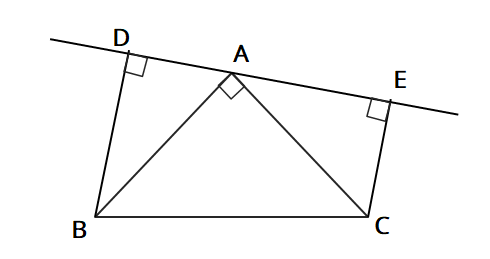



中2数学 直角三角形の合同の証明 応用問題 中学生勉強サイトあかね先生




二等辺三角形になることの証明 Youtube




中2数学 三角形の合同の証明応用問題 中学生勉強サイトあかね先生



全等三角形学好全等三角形有诀窍学霸不用课本完全靠它 我有车



构造等腰三角形 证明几何问题 杂志论文 理科考试研究



全等三角形的证明过程 西瓜视频搜索



三角形内角和定理 平行线的证明ppt 第2课时 第一ppt



构造等腰三角形 证明几何问题 杂志论文 理科考试研究




三角形と四角形 三角形の合同の証明のしかた 中学数学 定期テスト対策サイト
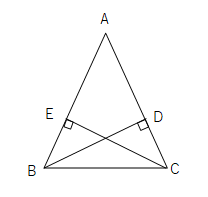



中2数学 直角三角形の合同証明のポイントと練習問題 Examee



中考数学 费马点 问题 王者再度归来




最も人気のある 三角形合同証明 ニスヌーピー壁紙



Ssa能证明全等吗 西瓜视频搜索




所有三角形都是等腰三角形 证明竟然无漏洞 问题出在哪里 每日头条



全等三角形学好全等三角形有诀窍学霸不用课本完全靠它 我有车



Studydoctor三角形の合同の証明 応用 中2数学 Studydoctor




八年级上册第十三章轴对称等腰三角形的判定湖北省通山县教育局教研室袁观六 Ppt Download




中二 数学 直角三角形の合同 この証明問題の の意味がわかりません W Clear



证明两个三角形全等的基本思路第2怎么写 信息图文欣赏 信息村 K0w0m Com



四边形的几何证明问题比较灵活 认真分析解题思路是关键 3u文域
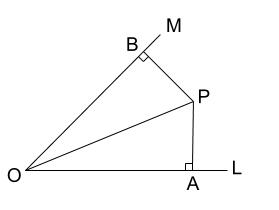



中学数学 直角三角形の合同の証明 中学数学の無料オンライン学習サイトchu Su




中2数学 二等辺三角形の証明 練習編 映像授業のtry It トライイット




三角形の合同証明の練習 無料で使える中学学習プリント



三角形在生活中的应用 图片信息欣赏 图客 Tukexw Com



合同な図形 三角形の証明問題 苦手な数学を簡単に



动点定角问题 证明垂直 正方形 箭型全等 直角三角形斜边上的中线 哔哩哔哩 Bilibili



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋



三角形三个角之和为180 西瓜视频搜索




平面几何 一大类角格点问题的统一证明 百度经验




三角形の合同条件を使った証明問題 中学2年生の問題を解こう 身勝手な主張



中学数学 三角形の合同の証明 その2 中学数学の無料オンライン学習サイトchu Su



初中数学几何神书 平几纲目第三卷1 中 3u文域




直角三角形邊長角度三角形 Dwfne



初中数学几何神书 平几纲目第三卷1 中 3u文域



等边三角形中的三垂线问题 天天教你学数学 微信公众号文章阅读 Wemp




三角形全等的判定定理证明过程




最も人気のある 三角形合同証明 ニスヌーピー壁紙




三角形の相似条件と証明問題の解き方 数学fun
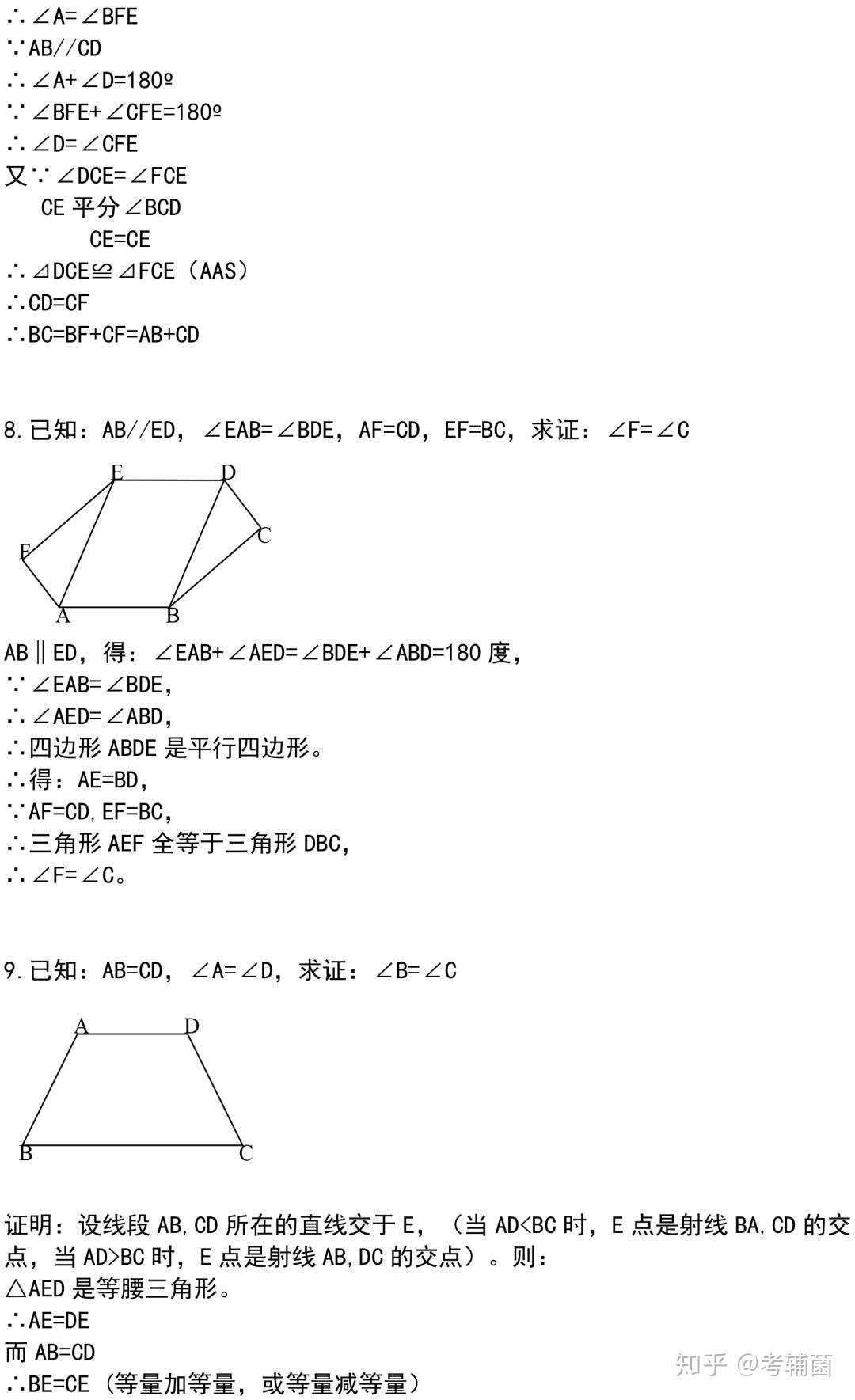



44道经典的三角形证明题 全部做完期末证明题满分 还不来看 知乎



Studydoctor三角形の合同証明の進め方 中2数学 Studydoctor



0 件のコメント:
コメントを投稿