3ステップでわかる 立方体 正六面体 の展開図の書き方 解き方 Qikeru 学びを楽しくわかりやすく
立方体 Created Date PM空間図形 投影図 166 1 次のア～イに入る言葉を右下の答えのらんに書きましょう。 2 次の図のように円柱を置くとき、立面図と平面図はそれぞれ どんな図形になりますか。言葉や名称で答えなさい。 立体を平面上に表す方法として、見取り図や展開図の他に、立体をある方向から
正 六面体 展開 図
正 六面体 展開 図-上中図のように、この展開図からできる立体は2種類あります。 1つは 右上図の同じ色で示した辺を付け、点線を谷折りにして出来る、 (図は デルタ六面体(正四面体2個合わせた立体)2個を色分けしていま正多面体は、正四面体、正六面体、正八面体、正12面体、正面体の5種類しかない。 正四面体と立方体は簡単にできる。 これをもとに、他の立体を作図してみよう。 まずネットでそれぞれの多面体を調べてみよう。 どう作図できるか浮かんでくる。
立方体の展開図は何種類ある 難関中学の受験に役立つ基礎知識 富裕層向け資産防衛メディア 幻冬舎ゴールドオンライン
★ 正四面体 ★ 正三角形4面に囲まれた立体。 辺の数：6本。 頂点の数：4個。 展開図（クリックすると別ウィンドウで印刷用ファイルが開きます。） 「シンプル イズ ベスト」ですねぇ。・・・美しいわ。 次は、組立図です。第1章「のりを使わない正十二面体・正二十面体の展開図」 33c 32d 26a 12b 11a 22c 33a 32b 31c 33d 24a 13b 12a 23b 31a 33b 22b 25c 23a 26b 21a 24b 22a 25b 32c 31d 25a 11b 13a 21b 32a 31b 31c35a 24b23c 22b22c 31d35b 25a24a 12b11a 21d21d 32c31a 25b24c 23b23c 32d31b 21a25a 13b12a 22d22d 33c32a 21b25c 24b24c 33d32b 22a21a エンジュニアクラブS 11月 正多面体と平行六面体小物入れ こんにちは！ クシローネです。 11月のエンジュニアクラブのレポートでーす。 今回は学生スタッフもついて、細かくサポートしてくれたよ。 前回は正三、四、五角形のお話だったね、今回は
Title 正六面体 Created Date AMそれでは、冒頭の図のような6面図の作り方を説明します。 これもアニメーションを使っての説明になりますので、ブラウザの更新ボタンで最初からご覧ください。 2破線 冒頭の6面図では、破線（はせん右図点滅の線）が現れています。 これは正四面体を切り開いて得られる展開図は無数の異なる図形になり得ます．しかし，この 定理が保証していることは，それがどんな形であっても平面をタイル張りするということ です． 四面体タイル定理4 正四面体のいかなる展開図もタイル張り可能である．
正 六面体 展開 図のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
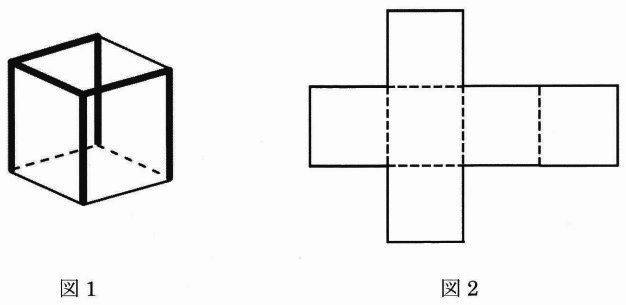 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |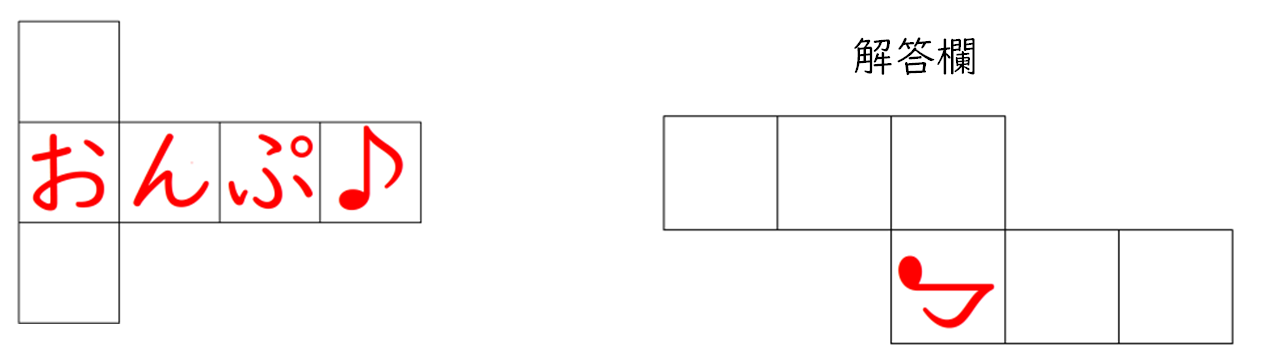
 立方体の展開図 奇々怪々なる塾解析 | 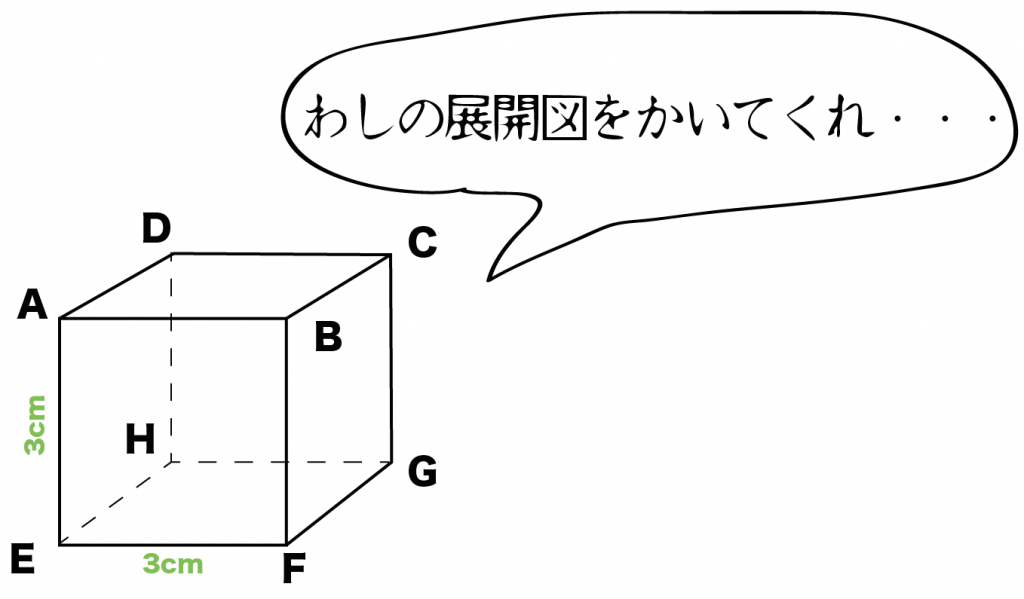 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 | 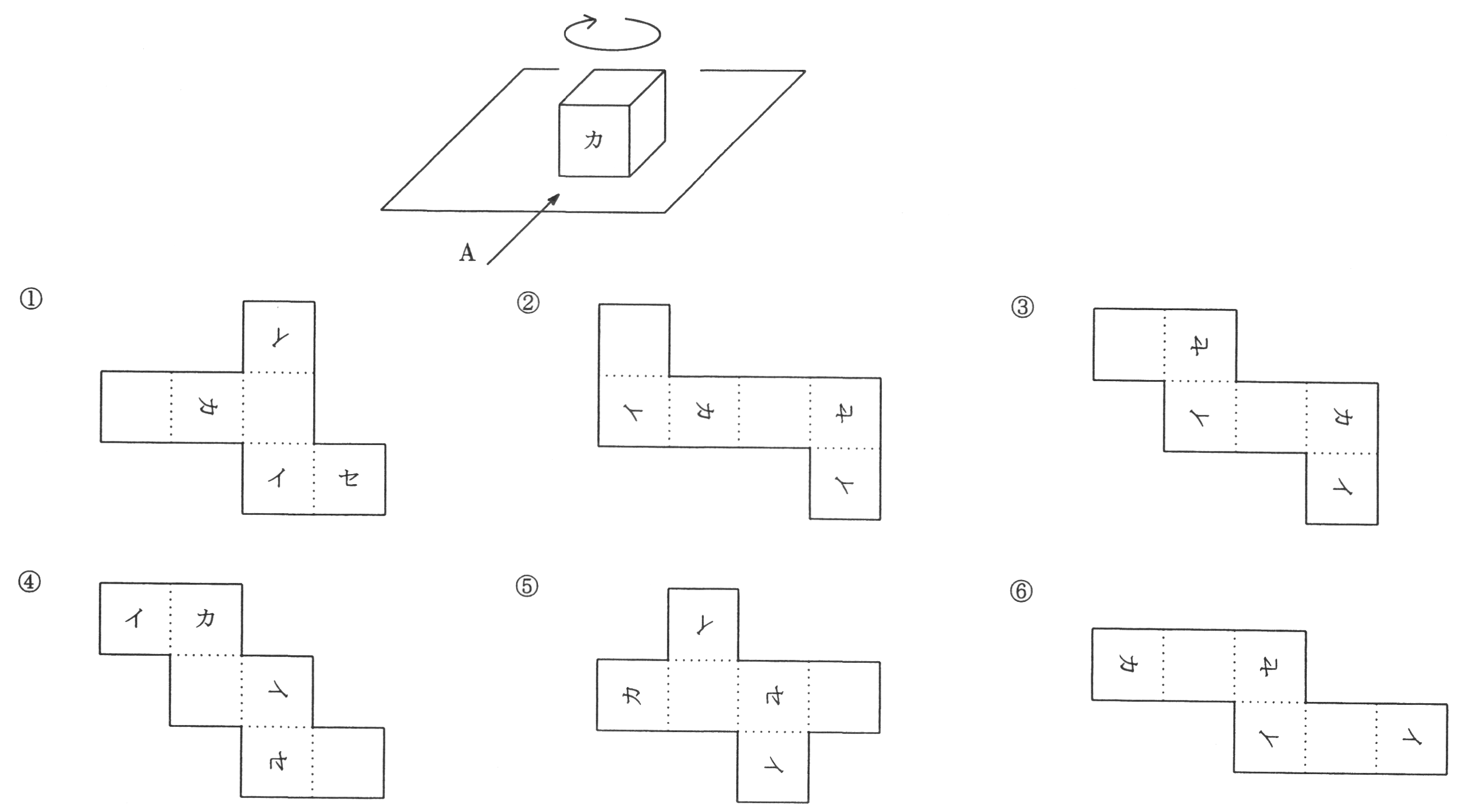 立方体の展開図 奇々怪々なる塾解析 |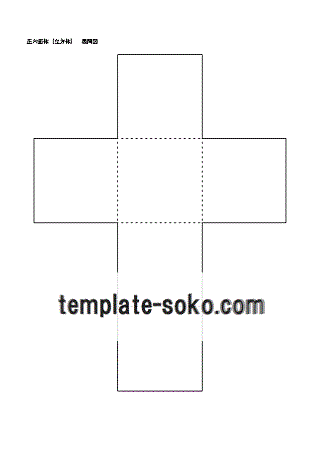
 立方体の展開図 奇々怪々なる塾解析 | 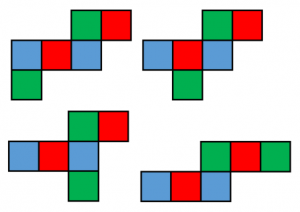 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |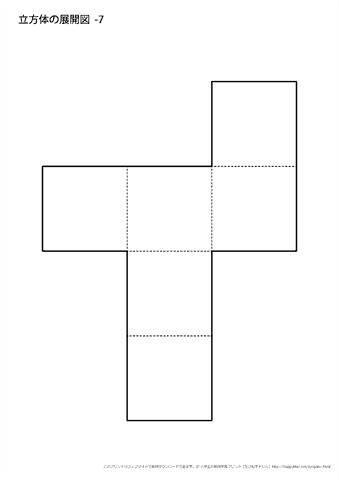
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  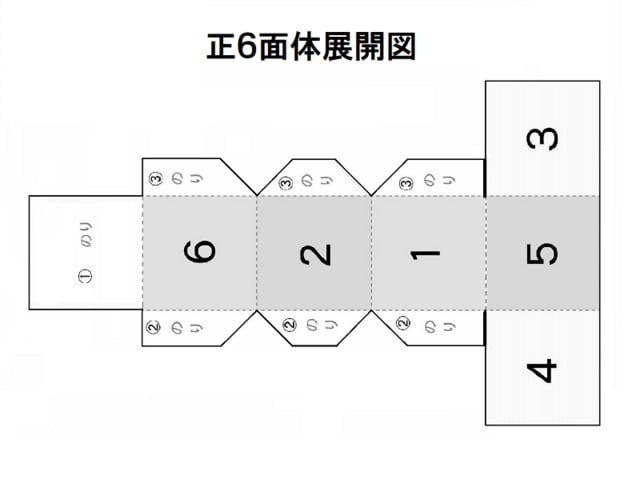立方体の展開図 奇々怪々なる塾解析 |
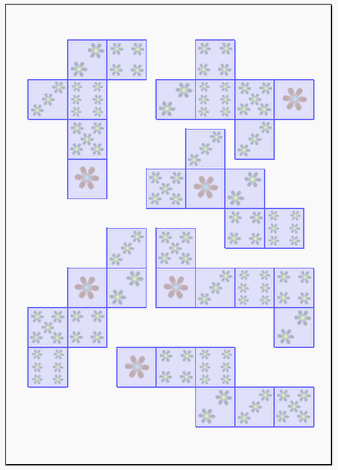 立方体の展開図 奇々怪々なる塾解析 | 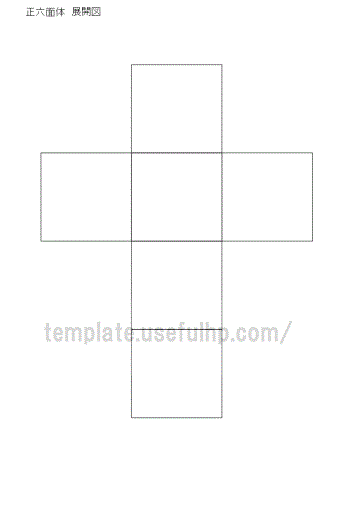 立方体の展開図 奇々怪々なる塾解析 | 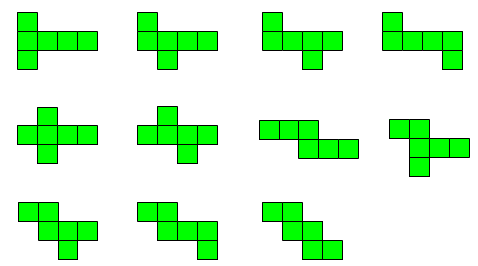 立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 | 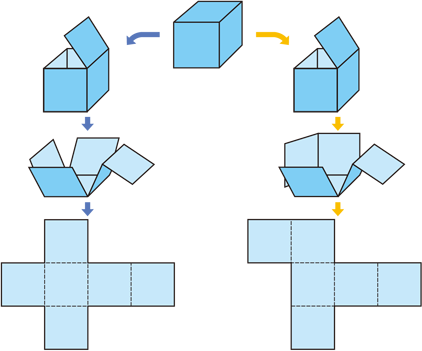 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |
立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |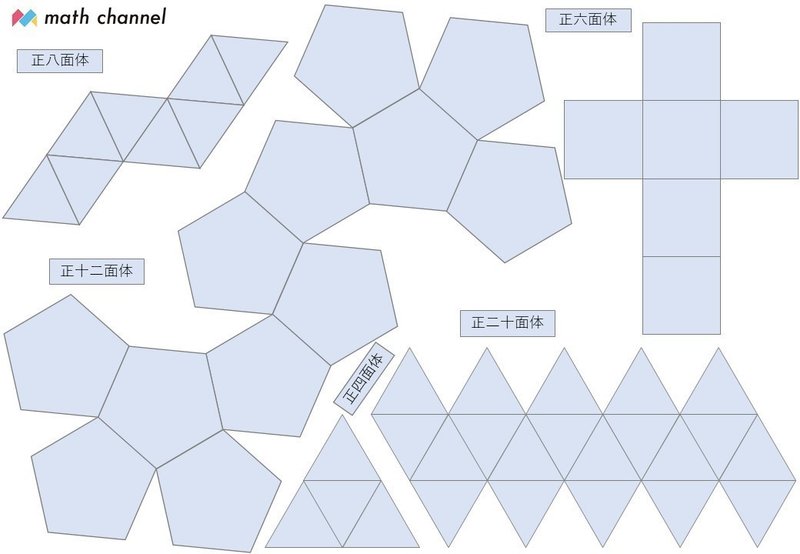
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |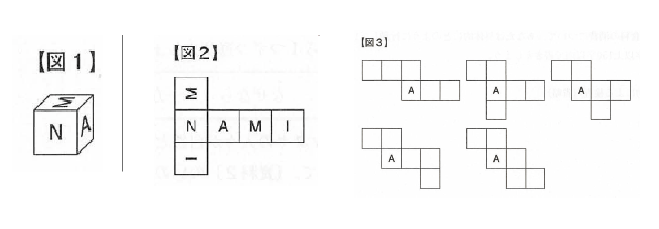
 立方体の展開図 奇々怪々なる塾解析 | 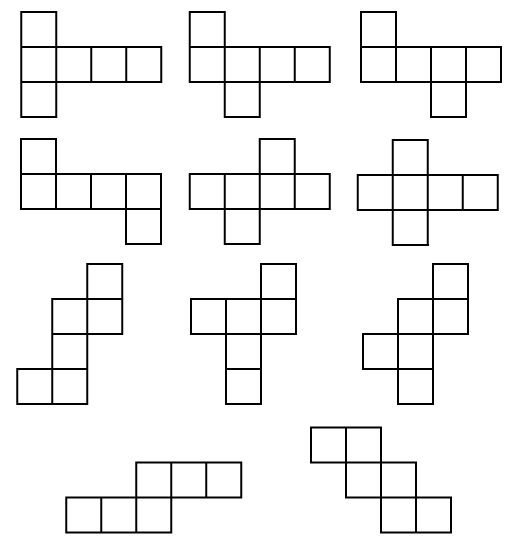 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |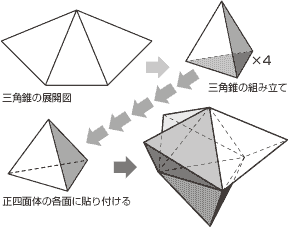
立方体の展開図 奇々怪々なる塾解析 | 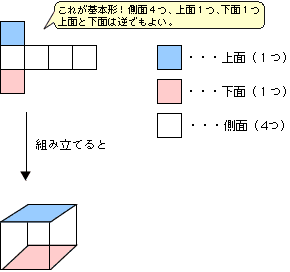 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 | 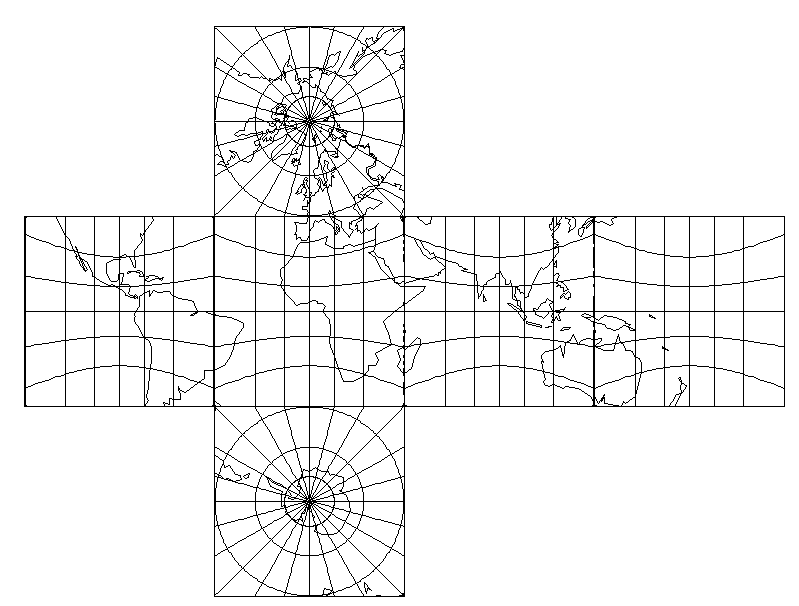 立方体の展開図 奇々怪々なる塾解析 |
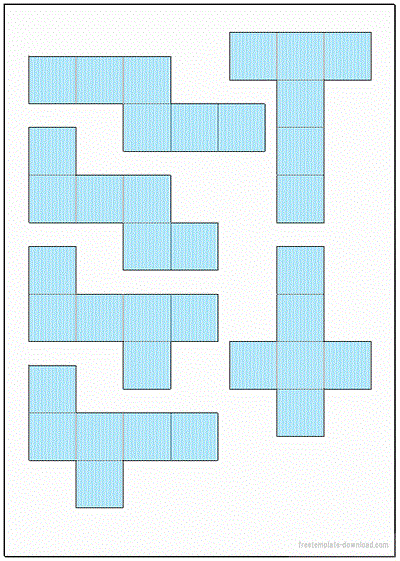 立方体の展開図 奇々怪々なる塾解析 | 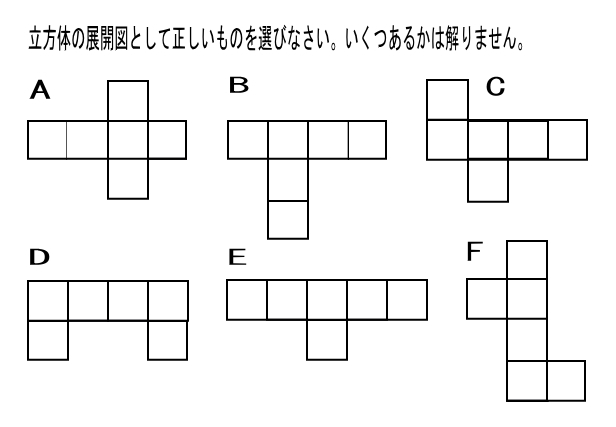 立方体の展開図 奇々怪々なる塾解析 | 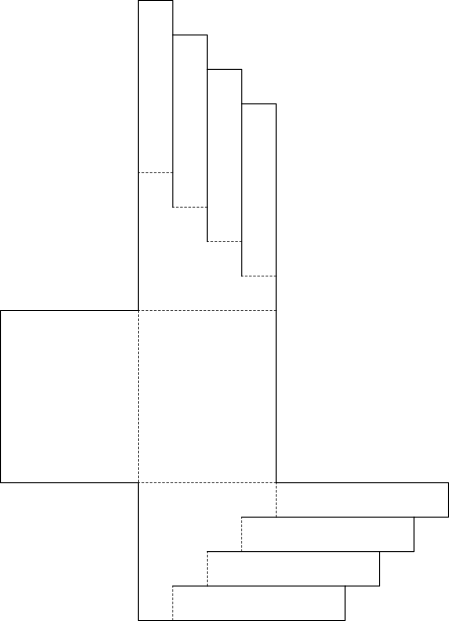 立方体の展開図 奇々怪々なる塾解析 |
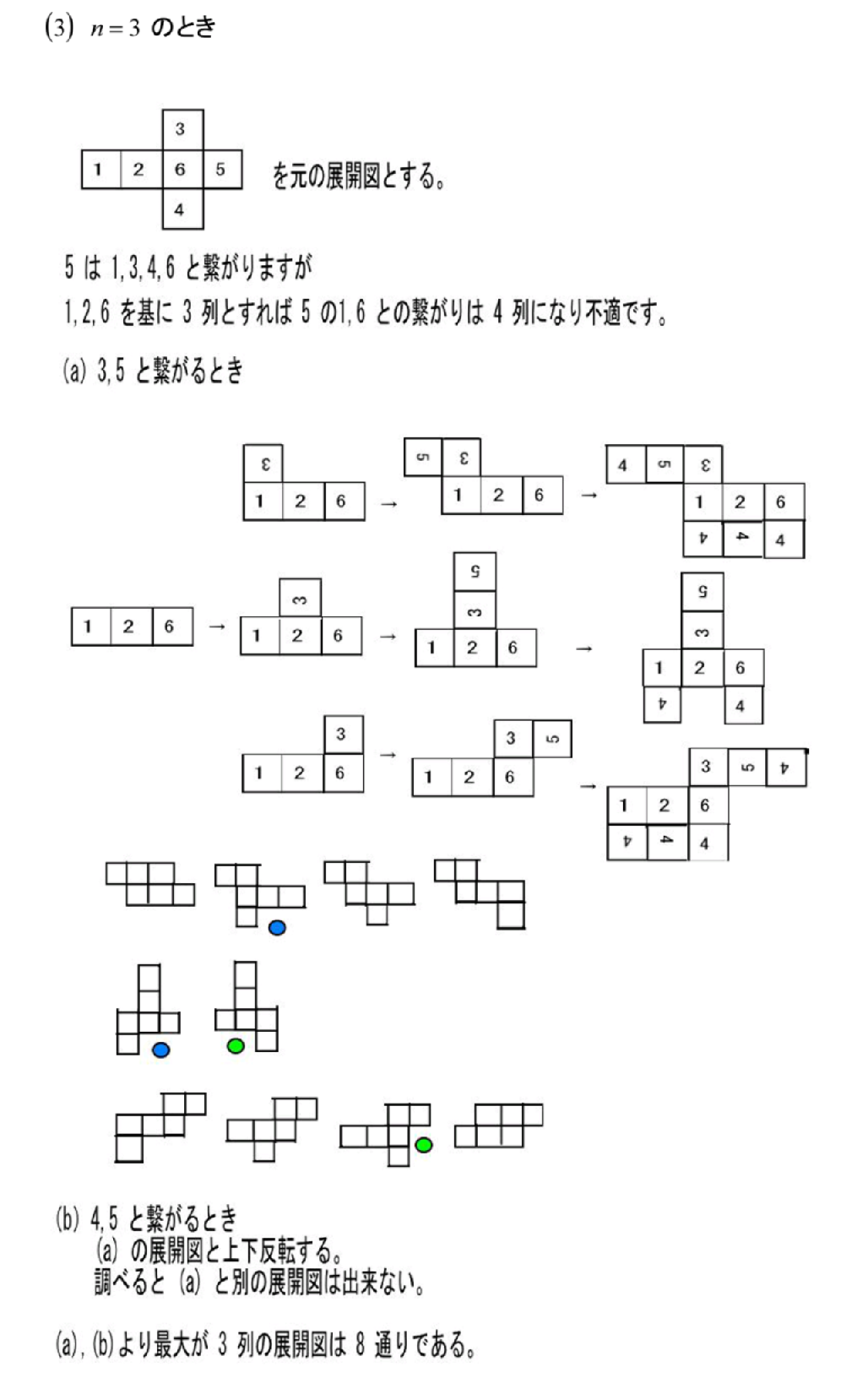 立方体の展開図 奇々怪々なる塾解析 | 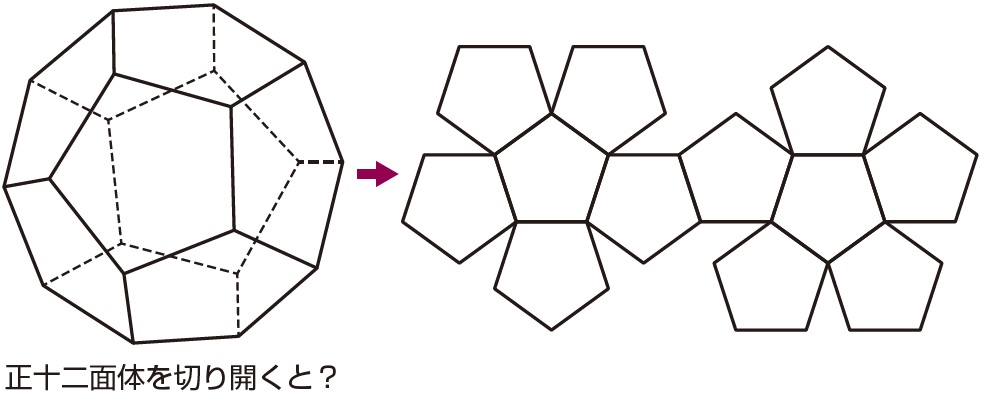 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 | 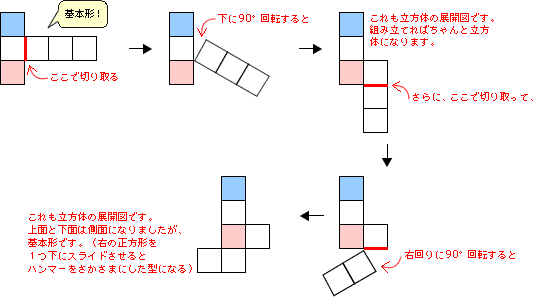 立方体の展開図 奇々怪々なる塾解析 |
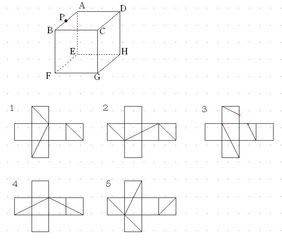 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |
立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 | 立方体の展開図 奇々怪々なる塾解析 |
立方体の展開図 奇々怪々なる塾解析 |  立方体の展開図 奇々怪々なる塾解析 |
小星形十二面体 この星形は、正十二面体の各面にご五角錐をくっつけてできるものです。 逆にこのとげとげを切り落とすと、正十二面体になります。 展開図 こんにちは。相城です。正八面体に関してです。平行な辺の見つけ方です。 下の図のような正八面体の展開図があり, 辺EBと平行な辺はどれか答えなさい。この問題に あなたは即座に答えられますか？答えは辺DCです。実は決まりがあ
0 件のコメント:
コメントを投稿